Page 235 - DECO401_MICROECONOMIC_THEORY_ENGLISH

Microeconomic Theory

Notes
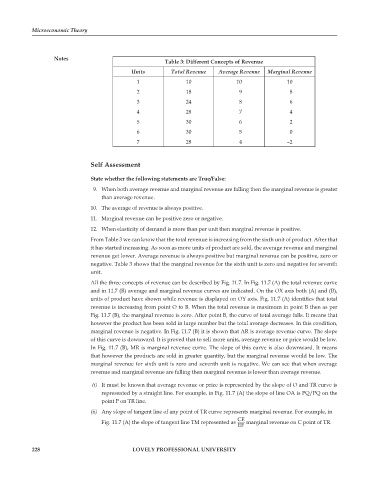
Table 3: Different Concepts of Revenue
Units Total Revenue Average Revenue Marginal Revenue
1 10 10 10
2 18 9 8
3 24 8 6
4 28 7 4
5 30 6 2
6 30 5 0
7 28 4 –2

Self Assessment

State whether the following statements are True/False:
9. When both average revenue and marginal revenue are falling then the marginal revenue is greater
than average revenue.
10. The average of revenue is always positive.
11. Marginal revenue can be positive zero or negative.
12. When elasticity of demand is more than per unit then marginal revenue is positive.

From Table 3 we can know that the total revenue is increasing from the sixth unit of product. After that
it has started increasing. As soon as more units of product are sold, the average revenue and marginal
revenue get lower. Average revenue is always positive but marginal revenue can be positive, zero or
negative. Table 3 shows that the marginal revenue for the sixth unit is zero and negative for seventh
unit.

All the three concepts of revenue can be described by Fig. 11.7. In Fig. 11.7 (A) the total revenue curve
and in 11.7 (B) average and marginal revenue curves are indicated. On the OX axis both (A) and (B),
units of product have shown while revenue is displayed on OY axis. Fig. 11.7 (A) identifies that total
revenue is increasing from point O to B. When the total revenue is maximum in point B then as per
Fig. 11.7 (B), the marginal revenue is zero. After point B, the curve of total average falls. It means that
however the product has been sold in large number but the total average decreases. In this condition,
marginal revenue is negative. In Fig. 11.7 (B) it is shown that AR is average revenue curve. The slope
of this curve is downward. It is proved that to sell more units, average revenue or price would be low.
In Fig. 11.7 (B), MR is marginal revenue curve. The slope of this curve is also downward. It means
that however the products are sold in greater quantity, but the marginal revenue would be low. The
marginal revenue for sixth unit is zero and seventh unit is negative. We can see that when average
revenue and marginal revenue are falling then marginal revenue is lower than average revenue.

(i) It must be known that average revenue or price is represented by the slope of O and TR curve is
represented by a straight line. For example, in Fig. 11.7 (A) the slope of line OA is PQ/PQ on the
point P on TR line.
(ii) Any slope of tangent line of any point of TR curve represents marginal revenue. For example, in
CE

Fig. 11.7 (A) the slope of tangent line TM represented as ___ marginal revenue on C point of TR.
EF

228 LOVELY PROFESSIONAL UNIVERSITY