Page 414 - DECO401_MICROECONOMIC_THEORY_ENGLISH

Unit-29: Insurance Choice and Risk

_____________
n
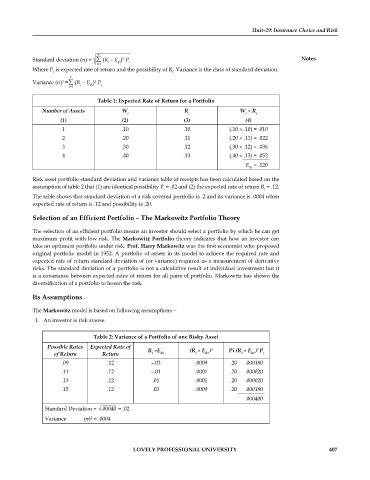
Standard deviation (σ) = ∑ (R – E ) P Notes
2
√ i=1 i Ri i
Where P is expected rate of return and the possibility of R . Variance is the class of standard deviation.
i i
n
2
2
Variance (σ) = ∑ (R – E ) P
i=1 i Ri i
Table 1: Expected Rate of Return for a Portfolio
Number of Assets W R W × R
i i i i
(1) (2) (3) (4)
1 .10 .10 (.10 × .10) = .010
2 .20 .11 (.20 × .11) = .022
3 .30 .12 (.30 × .12) = .036
4 .40 .13 (.40 × .13) = .052
E = .120
Ri
Risk asset portfolio standard deviation and variance table of receipts has been calculated based on the
assumption of table 2 that (1) are identical possibility P = .02 and (2) the expected rate of return R = .12.
i i
The table shows that standard deviation of a risk covered portfolio is .2 and its variance is .0004 when
expected rate of return is .12 and possibility is .20.

Selection of an Efficient Portfolio – The Markowitz Portfolio Theory

The selection of an efficient portfolio means an investor should select a portfolio by which he can get
maximum profit with low risk. The Markowitz Portfolio theory indicates that how an investor can
take an optimum portfolio under risk. Prof. Harry Markowitz was the first economist who proposed
original portfolio model in 1952. A portfolio of assets in its model to achieve the required rate and
expected rate of return standard deviation of (or variance) required as a measurement of derivative
risks. The standard deviation of a portfolio is not a calculative result of individual investment but it
is a covariance between expected rates of return for all pairs of portfolio. Markowitz has shown the
diversification of a portfolio to lessen the risk.
Its Assumptions

The Markowitz model is based on following assumptions—
1. An investor is risk averse.

Table 2: Variance of a Portfolio of one Risky Asset
Possible Rates Expected Rate of R –E (R – E ) 2 Pi (R – E ) P
2
of Return Return i Ri i Ri i Ri i
.09 .12 –.03 .0009 .20 .000180
.11 .12 –.01 .0001 .20 .000020
.13 .12 .01 .0001 .20 .000020
.15 .12 .03 .0009 .20 .000180
.000400
______
Standard Deviation = √.00040 = .02

Variance (σ) = .0004
2

LOVELY PROFESSIONAL UNIVERSITY 407