Page 172 - DECO503_INTERNATIONAL_TRADE_AND_FINANCE_ENGLISH

International Trade and Finance

Notes coefficients in the F – S t + 1 regressions are more than two standard errors above 0.0, but only one
t
(Belgium) is more than two standard errors above 1.0. Equivalently, only one of the negative slope
coefficients in the S – S regressions (Belgium) is more than two standard errors below zero. Perhaps
t+ 1 t
the appropriate conclusion is that all variation through time in F – S is variation in premiums, and
t
t
there is no variation in expected changes in spot rates.
Individually testing the β coefficients in table 2 against 1.0 (or the β coefficients against 0.0) does
1
2
not provide the appropriate joint test that all β = 1.0 (or all β = 0). An appropriate joint test takes
1
2
into account the high correlation of F – S t + 1 (or S t + 1 – S ) across currencies, documented in table 3.
t
t
Such cross-correlation is to be expected given that (a) all exchange rates are measured relative to the
U.S. dollar, and (b) most of the European countries are involved in attempts to control the movements
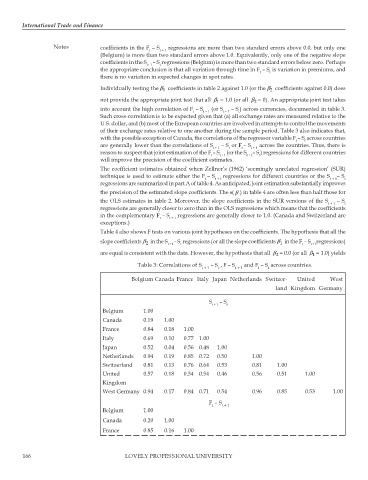
of their exchange rates relative to one another during the sample period. Table 3 also indicates that,
with the possible exception of Canada, the correlations of the regressor variable F – S across countries
t t
are generally lower than the correlations of S t + 1 – S or F – S t + 1 across the countries. Thus, there is
t
t
reason to suspect that joint estimation of the F – S t + 1 (or the S t + 1 – S ) regressions for different countries
t
t
will improve the precision of the coefficient estimates.
The coefficient estimates obtained when Zellner’s (1962) ‘seemingly unrelated regression’ (SUR)
technique is used to estimate either the F – S t + 1 regressions for different countries or the S t + 1 – S t
t
regressions are summarized in part A of table 4. As anticipated, joint estimation substantially improves
the precision of the estimated slope coefficients. The s( β ) in table 4 are often less than half those for
the OLS estimates in table 2. Moreover, the slope coefficients in the SUR versions of the S t + 1 – S t
regressions are generally closer to zero than in the OLS regressions which means that the coefficients
in the complementary F – S regressions are generally closer to 1.0. (Canada and Switzerland are
t t + 1
exceptions.)
Table 4 also shows F tests on various joint hypotheses on the coefficients. The hypothesis that all the
slope coefficients β in the S – S regressions (or all the slope coefficients β in the F – S regressions)
2
1
t + l
t
t + l
t
are equal is consistent with the data. However, the hypothesis that all β = 0.0 (or all β = 1.0) yields
1
2
Table 3: Correlations of S – S , F – S and F – S across countries.
t + 1 t t + 1 t t
Belgium Canada France Italy Japan Netherlands Switzer- United West
land Kingdom Germany
S – S
t + 1 t
Belgium 1.00
Canada 0.19 1.00
France 0.84 0.18 1.00
Italy 0.69 0.10 0.77 1.00
Japan 0.52 0.04 0.56 0.48 1.00
Netherlands 0.94 0.19 0.85 0.72 0.50 1.00
Switzerland 0.81 0.13 0.76 0.64 0.53 0.81 1.00
United 0.57 0.18 0.54 0.54 0.46 0.56 0.51 1.00
Kingdom
West Germany 0.94 0.17 0.84 0.71 0.54 0.96 0.85 0.53 1.00
F – S t + 1
t
Belgium 1.00
Canada 0.20 1.00
France 0.85 0.16 1.00

166 LOVELY PROFESSIONAL UNIVERSITY