Page 117 - DECO504_STATISTICAL_METHODS_IN_ECONOMICS_ENGLISH

Unit 7: Mean Deviation and Standard Deviation

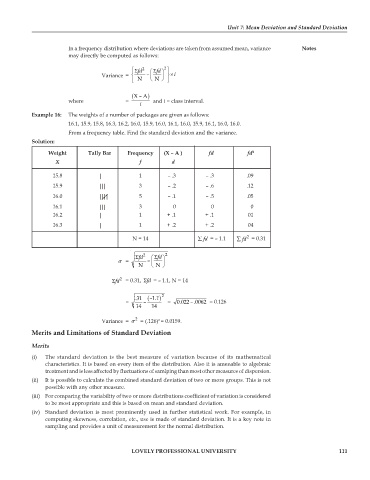
In a frequency distribution where deviations are taken from assumed mean, variance Notes
may directly be computed as follows:

⎧ ⎪ Σ 2 ⎛ Σfd ⎞ fd 2 ⎫ ⎪
Variance = ⎨ – ⎜ ⎟ ⎬ × i
⎪ ⎝ N ⎠ N ⎪ ⎩ ⎭

( )X – A
where = and i = class interval.
i
Example 16: The weights of a number of packages are given as follows:
16.1, 15.9, 15.8, 16.3, 16.2, 16.0, 15.9, 16.0, 16.1, 16.0, 15.9, 16.1, 16.0, 16.0.
From a frequency table. Find the standard deviation and the variance.
Solution:

Weight Tally Bar Frequency (X – A ) fd fd 2
X f d

15.8 1 – .3 – .3 .09
15.9 3 – .2 – .6 .12
16.0 5 – .1 – .5 .05
16.1 3 0 0 0
16.2 1 + .1 + .1 01
16.3 1 + .2 + .2 04
2
N = 14 ∑ fd = – 1.1 ∑ fd = 0.31

Σfd 2 ⎛ Σ ⎞ fd 2
σ = – ⎜ ⎟
⎝ N ⎠ N

Σfd 2 = 0.31, Σfd = – 1.1, N = 14

( .31 )–1.1 2
= – = 0.022 – .0062 = 0.126
14 14
2
Variance = σ = (.126) = 0.0159.
2
Merits and Limitations of Standard Deviation

Merits
(i) The standard deviation is the best measure of variation because of its mathematical
characteristics. It is based on every item of the distribution. Also it is amenable to algebraic
treatment and is less affected by fluctuations of samlping than most other measures of dispersion.
(ii) It is possible to calculate the combined standard deviation of two or more groups. This is not
possible with any other measure.
(iii) For comparing the variability of two or more distributions coefficient of variation is considered
to be most appropriate and this is based on mean and standard deviation.
(iv) Standard deviation is most prominently used in further statistical work. For example, in
computing skewness, correlation, etc., use is made of standard deviation. It is a key note in
sampling and provides a unit of measurement for the normal distribution.

LOVELY PROFESSIONAL UNIVERSITY 111