Page 115 - DECO504_STATISTICAL_METHODS_IN_ECONOMICS_ENGLISH

Unit 7: Mean Deviation and Standard Deviation

The average marks obtained by P are higher. Hence his performance is better. The Notes
coefficient of variation is lower in case of P hence he is a more consistent student.
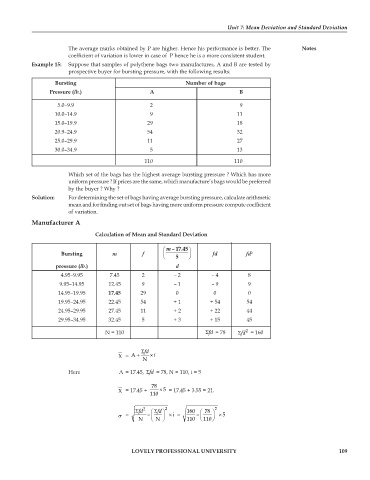
Example 15: Suppose that samples of polythene bags two manufactures, A and B are tested by
prospective buyer for bursting pressure, with the following results:
Bursting Number of bags
Pressure (lb.) A B

5.0–9.9 2 9
10.0–14.9 9 11
15.0–19.9 29 18
20.9–24.9 54 32
25.0–29.9 11 27
30.0–34.9 5 13
110 110

Which set of the bags has the highest average bursting pressure ? Which has more
uniform pressure ? If prices are the same, which manufacture’s bags would be preferred
by the buyer ? Why ?
Solution: For determining the set of bags having average bursting pressure, calculate arithmetic
mean and for finding out set of bags having more uniform pressure compute coefficient
of variation.
Manufacturer A

Calculation of Mean and Standard Deviation

⎛ – 17.45 ⎞ m
Bursting m f ⎜ ⎟ fd fd 2
⎝ 5 ⎠
pressure (lb.) d
4.95–9.95 7.45 2 – 2 – 4 8
9.95–14.95 12.45 9 – 1 – 9 9
14.95–19.95 17.45 29 0 0 0
19.95–24.95 22.45 54 + 1 + 54 54
24.95–29.95 27.45 11 + 2 + 22 44
29.95–34.95 32.45 5 + 3 + 15 45

2
N = 110 Σfd = 78 Σfd = 160

Σfd
X = A + × i
N
Here A = 17.45, fdΣ = 78, N = 110, i = 5

78
X = 17.45 + 110 × 5 = 17.45 + 3.55 = 21.

Σ fd 2 ⎛ Σ fd ⎞ 2 160 ⎛ 78 ⎞ 2
σ = – ⎜ ⎟ i × = – ⎜ ⎟ × 5
N ⎝ N ⎠ 110 ⎝ 110 ⎠

LOVELY PROFESSIONAL UNIVERSITY 109