Page 165 - DECO504_STATISTICAL_METHODS_IN_ECONOMICS_ENGLISH

Unit 10: Correlation: Scatter Diagram Method, Karl Pearson's Coefficient of Correlation

(vi) Take the squares of the deviations of the variable X and multiply them by the respective Notes

frequencies and obtain ∑ fd 2 .
x
(vii) Multiply the frequencies of the variable Y by the deviations of Y and obtain the total ∑ fd .
y
(viii) Take the squares of the deviations of the variable Y and multiply them by the respective
frequencies and obtain ∑ fd y 2 .

,
(ix) Substitute the values of ∑ fdd , ∑ fd , ∑ fd x 2 ∑ fd and ∑ fd y 2 in the above formula and
y
y
x
x
obtain the value of r.
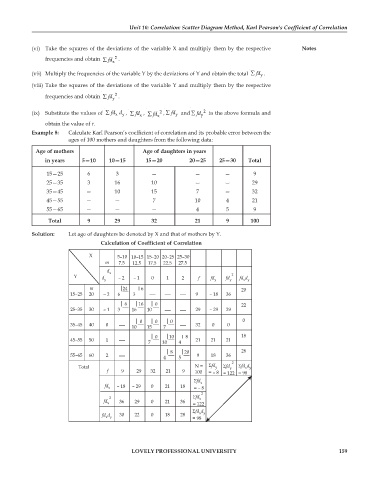
Example 8: Calculate Karl Pearson’s coefficient of correlation and its probable error between the
ages of 100 mothers and daughters from the following data:
Age of mothers Age of daughters in years
in years 5—10 10—15 15—20 20—25 25—30 Total
15—25 6 3 — — — 9
25—35 3 16 10 — — 29
35—45 — 10 15 7 — 32
45—55 — — 7 10 4 21
55—65 — — — 4 5 9

Total 9 29 32 21 9 100

Solution: Let age of daughters be denoted by X and that of mothers by Y.
Calculation of Coefficient of Correlation

X 5–10 10–15 15–20 20–25 25–30
m 7.5 12.5 17.5 22.5 27.5
d x
Y d y –2 –1 0 1 2 f fd y fd y 2 fd d
x y
m 24 6 20
15–25 20 –2 6 3 9 – 18 36
6 16 0 22
25–35 30 –1 3 16 10 29 –29 29

0 0 0 0
35–45 40 0 10 15 7 32 0 0
0 10 8 18
45–55 50 1 21 21 21
7 10 4
8 20 28
55–65 60 2 9 18 36
4 5
2
Total N= fd y fd y fd d
xy
f 9 29 32 21 9 100 =–8 = 122 =98
fd x
fd –18 –29 0 21 18
x =–8
2
2 fd x
fd 36 29 0 21 36
x = 122
fd d
xy
fd d 30 22 0 18 28
x y =98

LOVELY PROFESSIONAL UNIVERSITY 159