Page 163 - DECO504_STATISTICAL_METHODS_IN_ECONOMICS_ENGLISH

Unit 10: Correlation: Scatter Diagram Method, Karl Pearson's Coefficient of Correlation

Notes
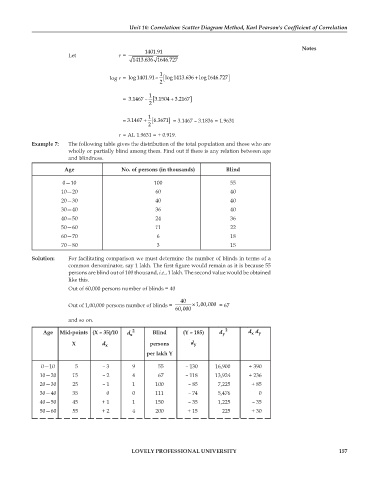
1401.91
Let r =
1413.636 1646.727

1
log r = log 1401.91 – [ + ]log1413.636 log 1646.727
2
1
= 3.1467 – [ + ]3.1504 3.2167
2
1
= 3.1467 + [ ]6.3671 = 3.1467 – 3.1836 = 1.9631
2
r = AL 1.9631 = + 0.919.
Example 7: The following table gives the distribution of the total population and those who are
wholly or partially blind among them. Find out if there is any relation between age
and blindness.
Age No. of persons (in thousands) Blind

0—10 100 55
10—20 60 40
20—30 40 40
30—40 36 40
40—50 24 36
50—60 11 22
60—70 6 18
70—80 3 15

Solution: For facilitating comparison we must determine the number of blinds in terms of a
common denominator, say 1 lakh. The first figure would remain as it is because 55
persons are blind out of 100 thousand, i.e., 1 lakh. The second value would be obtained
like this.
Out of 60,000 persons number of blinds = 40
40
Out of 1,00,000 persons number of blinds = × 1,00,000 = 67
60,000
and so on.

Age Mid-points (X – 35)/10 d x 2 Blind (Y – 185) d y 2 dd y
x
X d x persons d y
per lakh Y

0—10 5 – 3 9 55 – 130 16,900 + 390
10—20 15 – 2 4 67 – 118 13,924 + 236
20—30 25 – 1 1 100 – 85 7,225 + 85
30—40 35 0 0 111 – 74 5,476 0
40—50 45 + 1 1 150 – 35 1,225 – 35
50—60 55 + 2 4 200 + 15 225 + 30

LOVELY PROFESSIONAL UNIVERSITY 157