Page 158 - DECO504_STATISTICAL_METHODS_IN_ECONOMICS_ENGLISH

Statistical Methods in Economics

Notes ∑xy
r =
∑ 2 ∑x y 2

2
2
∑xy = 431, ∑x = 598, ∑y = 338
431 431
r = = = + 0.959.
598 × 338 449.582
Example 3: Find coefficient of correlation for the following:

Cost (Rs.) 39 65 62 90 82 75 25 98 36 78

Sales (Rs.) 47 53 58 86 62 68 60 91 51 84

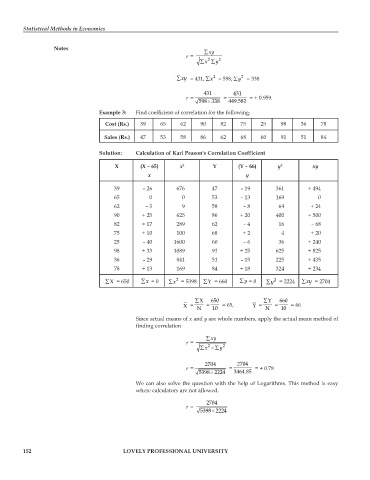
Solution: Calculation of Karl Peason's Correlation Coefficient

X (X – 65) x 2 Y (Y – 66) y 2 xy
x y
39 – 26 676 47 – 19 361 + 494
65 0 0 53 – 13 169 0
62 – 3 9 58 – 8 64 + 24
90 + 25 625 86 + 20 400 + 500
82 + 17 289 62 – 4 16 – 68
75 + 10 100 68 + 2 4 + 20
25 – 40 1600 60 – 6 36 + 240
98 + 33 1089 91 + 25 625 + 825
36 – 29 841 51 – 15 225 + 435
78 + 13 169 84 + 18 324 + 234
2
2
∑X = 650 ∑x = 0 ∑x = 5398 ∑Y = 660 ∑y = 0 ∑y = 2224 ∑xy = 2704
∑X 650 ∑Y 660
X = N = 10 = 65, Y = N = 10 = 66

Since actual means of x and y are whole numbers, apply the actual mean method of
finding correlation

∑xy
r =
∑ 2 ×x ∑ y 2

2704 2704
r = = = + 0.78
5398 × 2224 3464.85
We can also solve the question with the help of Logarithms. This method is easy
where calculators are not allowed.
2704
r =
5398 × 2224

152 LOVELY PROFESSIONAL UNIVERSITY