Page 188 - DECO504_STATISTICAL_METHODS_IN_ECONOMICS_ENGLISH

Statistical Methods in Economics

Notes Regression of X on Y :

The line of regression of X on Y using its regression coefficient is :
( − ) XX = YX ( b YY ) − ... (ii)

Σ NXY ( − )Σ ( Y )ΣX
Here, b YX = Σ NY 2 ( − Y )Σ 2

×
5 × − 214 30 40 1070 − 1200 130
= 2 = = − = – 1.30
5 × ( − 340 )40 1700 − 1600 100
b
Putting the value of X , Y and YX in equation (ii), the line of regression of X and Y becomes
(X – 6) = – 1.30 (Y – 8) or X = 6 – 1.30 Y + 10.4
or X + 1.30 Y = 16.4
which is also the same as obtained in example 1.
Remark
The two expression lines can be obtained by any of the above two methods if the values of the pairs
of observations are not very large. However, when the data are large, short cut method for computing
regression coefficient should be applied to avoid huge calculations. Calculations are further reduced if the
deviations of the two variables are taken from their respective means, i.e., when Σd and Σd are
y
x
zero. In this case, the regression coefficients YX and XY are obtained by using formula (7) and (14). The
b
b
example will on the next page clarify the point.
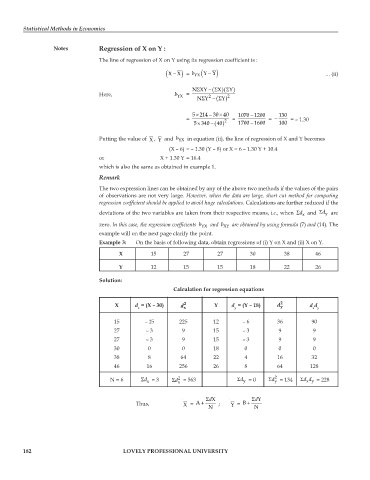
Example 3: On the basis of following data, obtain regressions of (i) Y on X and (ii) X on Y.
X 15 27 27 30 38 46
Y 12 15 15 18 22 26

Solution:
Calculation for regression equations

X d = (X – 30) d 2 Y d = (Y – 18) d 2 d d
x x y y x y

15 – 15 225 12 – 6 36 90
27 – 3 9 15 – 3 9 9
27 – 3 9 15 – 3 9 9
30 0 0 18 0 0 0
38 8 64 22 4 16 32
46 16 256 26 8 64 128
2
2
N = 6 Σd = 3 Σd = 563 Σd = 0 Σd = 134 Σdd = 228
y
x y
y
x
x
Σ X Σ Y
d
d
Thus, X = A + N ; Y = B + N

182 LOVELY PROFESSIONAL UNIVERSITY