Page 105 - DECO504_STATISTICAL_METHODS_IN_ECONOMICS_HINDI

bdkbZ—7% ekè; fopyu ,oa izeki fopyu

(a) lcls igys ml ekè; dks Kkr djrs gSa ftlls ekè; fopyu fudkyuk gksA uksV
(b) fiQj mlh ekè; ls chtxf.krh; fpÉksa dks NksM+rs gq, fofHkUu ewY;ksa ls fopyu |d| fudky fy;s
tkrs gSaA
(c) bu fopyuksa dks tksM+ ∑|d| fudky fy;k tkrk gSA
(d) fiQj fuEu lw=k dk iz;ksx djrs gSaμ
d
d
∑|d | ∑|| ∑||
δ = N M , δ x = N x , δ = N z
M
Z

ekè; fopyu xq.kkad fudkyus osQ fy, ekè; fopyu dks lEcfU/r ekè; ls Hkkx
ns fn;k tkrk gSA
mnkgj.k (Illustration) 1:
fuEu vk¡dM+ksa ls eè;dk ,oa lekUrj ekè; }kjk fopyu vkSj muosQ xq.kkad Kkr dhft,μ
47, 50, 58, 45, 53, 59, 47, 60, 49
gy (Solution):

lcls igys inewY;ksa dks vkjksgh Øe esa O;ofLFkr djosQ eè;dk ,oa lekUrj ekè; Kkr djrs gSa fiQj ekè;
fopyu dk ifjdyu djrs gSaA
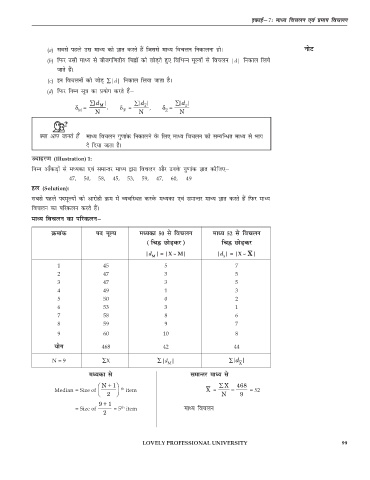
ekè; fopyu dk ifjdyuμ

Øekad in ewY; eè;dk 50 ls fopyu ekè; 52 ls fopyu
(fpÉ NksM+dj) fpÉ NksM+dj
|d | = |X – M| |d | = |X – X |
x
M
1 45 5 7
2 47 3 5
3 47 3 5
4 49 1 3
5 50 0 2
6 53 3 1
7 58 8 6
8 59 9 7
9 60 10 8

;ksx 468 42 44

N = 9 ∑X ∑|d | ∑ ||d X
M
eè;dk ls lekUrj ekè; ls
Median = Size of G F H N+ 1I J th item X = ∑ X = 468 = 52
2 K
N
9
9+ 1
th
= Size of = 5 item ekè; fopyu
2

LOVELY PROFESSIONAL UNIVERSITY 99