Page 111 - DECO504_STATISTICAL_METHODS_IN_ECONOMICS_HINDI

bdkbZ—7% ekè; fopyu ,oa izeki fopyu

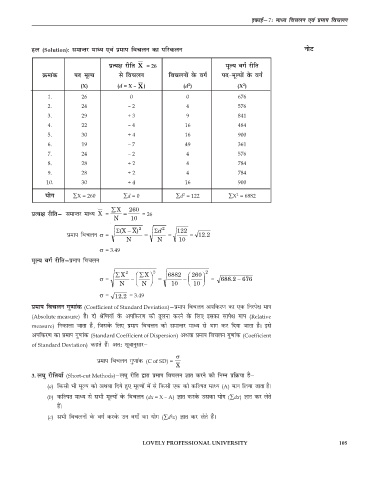
gy (Solution): lekUrj ekè; ,oa izeki fopyu dk ifjdyu uksV

izR;{k jhfr X = 26 ewY; oxZ jhfr
Øekad in ewY; ls fopyu fopyuksa osQ oxZ in&ewY;ksa osQ oxZ
2
2
(X) (d = X – X ) (d ) (X )
1. 26 0 0 676
2. 24 – 2 4 576
3. 29 + 3 9 841
4. 22 – 4 16 484
5. 30 + 4 16 900
6. 19 – 7 49 361
7. 24 – 2 4 576
8. 28 + 2 4 784
9. 28 + 2 4 784
10. 30 + 4 16 900

2
2
;ksx ∑X = 260 ∑d = 0 ∑d = 122 ∑X = 6882
∑ X 260
izR;{k jhfrμ lekUrj ekè; X = = = 26
N 10
Σ X) 2 Σ(X − d 2 122
izeki fopyu σ = = = = 12.2
N N 10
σ = 3.49
ewY; oxZ jhfrμizeki fopyu
∑ F I
260
∑ X 2 −G J 2 6882 F I 2
X
G J = 688.2 −
σ = H K = − H K 676
N N 10 10
σ = 12.2 = 3.49
izeki fopyu xq.kkad (Coefficient of Standard Deviation)μizeki fopyu vifdj.k dk ,d fujis{k eki
(Absolute measure) gSA nks Jsf.k;ksa osQ vifdj.k dh rqyuk djus osQ fy, bldk lkis{k eki (Relative
measure) fudkyk tkrk gS] ftlosQ fy, izeki fopyu dks lekUrj ekè; ls Hkkx dj fn;k tkrk gSA bls
vifdj.k dk izeki xq.kkad (Standard Coefficient of Dispersion) vFkok izeki fopyu xq.kkad (Coefficient

of Standard Deviation) dgrs gSaA vr% lw=kkuqlkjμ
σ
izeki fopyu xq.kkad (C of SD) =
X
3. y?kq jhfr;k¡ (Short-cut Methods)μy?kq jhfr }kjk izeki fopyu Kkr djus dh fuEu izfØ;k gSμ
(a) fdlh Hkh ewY; dks vFkok fn;s gq, ewY;ksa esa ls fdlh ,d dks dfYir ekè; (A) eku fy;k tkrk gSA

(b) dfYir ekè; ls lHkh ewY;ksa osQ fopyu (dx = X – A) Kkr djosQ mldk ;ksx (∑dx) Kkr dj ysrs
gSaA
2
(c) lHkh fopyuksa osQ oxZ djosQ mu oxks± dk ;ksx (∑d x) Kkr dj ysrs gSaA

LOVELY PROFESSIONAL UNIVERSITY 105