Page 168 - DECO504_STATISTICAL_METHODS_IN_ECONOMICS_HINDI

vFkZ'kkL=k esa lkaf[;dh; fof/;k¡

uksV x.kuk fØ;k,aμ
ljy izR;{k fof/ (Simple Direct Method)
mi;qZDr jhfr esa pkSFkh fØ;k esa crk;k x;k gS fd nksuksa Jsf.k;ksa osQ i`Fko~Q&i`Fko~Q izeki fopyu Kkr djus gksrs
gSa ftlesa dkiQh le; yxrk gSA vr% fi;lZu osQ lw=k esa σ vkSj σ osQ LFkku ij muosQ lw=k j[kdj bl dk;Z
y
x
dks vkSj ljy cuk;k tk ldrk gSA bl n'kk esa lw=k bl izdkj gksxkμ
/
Σdd N
r = x y (f}rh; lw=k)
Σd 2 x × Σd 2 y
N N

Σdd y Σdd y
x
x
rFkk r = ;k (r`rh; lw=k)
N Σ 2 Σd × d 2 Σ 2 Σd × d 2
N x y x y
Li"V gS fd rhuksa lw=kksa osQ }kjk ifj.kke leku vk;sxk D;ksafd rhuksa gh lw=k ewy lw=k osQ :i esa gSA r`rh; lw=k
vf/d ljy gS] vr% O;ogkj esa blh dk iz;ksx djuk pkfg,A
Σxy
fVIi.khμ;fn x = X – X rFkk y = Y – Y fy[kk tk;sxk rks r = fy[kk tk ldrk gSA
2
ΣΣ 2 y
x
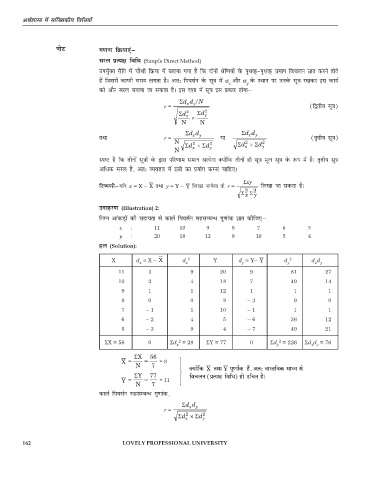
mnkgj.k (Illustration) 2:

fuEu vkadM+ksa dh lgk;rk ls dkyZ fi;lZu lglEcU/ xq.kkad Kkr dhft,μ
x : 11 10 9 8 7 6 5
y : 20 18 12 8 10 5 4
gy (Solution):

X d = X – X d x 2 Y d = Y– Y d y 2 d d
y
x
x y
11 3 9 20 9 81 27
10 2 4 18 7 49 14
9 1 1 12 1 1 1
8 0 0 8 – 3 9 0
7 – 1 1 10 – 1 1 1
6 – 2 4 5 – 6 36 12
5 – 3 9 4 – 7 49 21

2
ΣX = 56 0 Σd = 28 ΣY = 77 0 Σd = 226 Σd d = 76
2
x y
x
y
ΣX 56 U
X = = = 8
N 7 | V D;ksafd rFkk Y iw.kkZad gSa] vr% okLrfod ekè; ls
X
ΣY 77 | fopyu (izR;{k fof/) gh mfpr gA S
Y = N = 7 = 11 W
dkyZ fi;lZu lglEcU/ xq.kkad]
Σdd y
x
r =
Σ 2 x Σd × d 2 y

162 LOVELY PROFESSIONAL UNIVERSITY