Page 348 - DECO504_STATISTICAL_METHODS_IN_ECONOMICS_HINDI

vFkZ'kkL=k esa lkaf[;dh; fof/;k¡

uksV bl izdkj fofHkUu o"kks± osQ fy, laxf.kr fd;s x;s miufr ewY;ksa (84, 86, 88, 90, 92, 94 rFkk 96) dks fcUnq&js[kh;
i=k ij izkafdr djus ij tks oØ rS;kj gksxk mls izo`fÙk&js[kk dgsaxsA
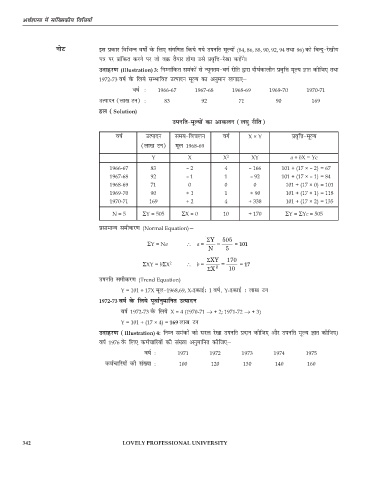
mnkgj.k (Illustration) 3: fuEukafdr leadksa ls U;wure&oxZ jhfr }kjk nh?kZdkyhu izo`fÙk ewY; Kkr dhft, rFkk
1972-73 o"kZ osQ fy;s lEHkkfor mRiknu ewY; dk vuqeku yxkb,μ
o"kZ : 1966-67 1967-68 1968-69 1969-70 1970-71
mRiknu (yk[k Vu) : 83 92 71 90 169
gy (Solution)

miufr&ewY;ksa dk vkdyu (y?kq jhfr)

o"kZ mRiknu le;&fopyu oxZ X × Y izo`fÙk&ewY;
(yk[k Vu) ewy 1968-69
Y X X 2 XY a + bX = Yc
1966-67 83 – 2 4 – 166 101 + (17 × – 2) = 67
1967-68 92 – 1 1 – 92 101 + (17 × – 1) = 84
1968-69 71 0 0 0 101 + (17 × 0) = 101
1969-70 90 + 1 1 + 90 101 + (17 × 1) = 118
1970-71 169 + 2 4 + 338 101 + (17 × 2) = 135
N = 5 ΣY = 505 ΣX = 0 10 + 170 ΣY = ΣYc = 505

izlkekU; lehdj.k (Normal Equation)—

ΣY 505
ΣY = Na ∴ a = = = 101
N 5
ΣXY 170
ΣXY = bΣX 2 ∴ b = = = 17
ΣX 2 10
miufr lehdj.k (Trend Equation)

Y = 101 + 17X ewy&1968,69, X-bdkbZ% 1 o"kZ] Y-bdkbZ % yk[k Vu
1972-73 o"kZ osQ fy;s iwokZuqekfur mRiknu
o"kZ 1972-73 osQ fy;s X = 4 (1970-71 → + 2; 1971-72 → + 3)
Y = 101 + (17 × 4) = 169 yk[k Vu
mnkgj.k (Illustration) 4: fuEu leadksa dks ljy js[kk miufr iznku dhft, vkSj miufr ewY; Kkr dhft,A
o"kZ 1976 osQ fy, deZpkfj;ksa dh la[;k vuqekfur dhft,μ
o"kZ : 1971 1972 1973 1974 1975
deZpkfj;ksa dh la[;k : 100 120 130 140 160

342 LOVELY PROFESSIONAL UNIVERSITY