Page 351 - DECO504_STATISTICAL_METHODS_IN_ECONOMICS_HINDI

bdkbZ—24% dky&Js.kh dh fof/ % U;wure oxZ jhfr osQ fl¼kar ,oa mlosQ vuqiz;ksx

Solution. pw¡fd fopyuksa dk ;ksx 'kwU; ugha gS vFkkZr ΣX ≠ 0 vr% ‘a’ rFkk ‘b’ dk eku izR;{k :i ls izlkekU; uksV
lehdj.kksa }kjk izkIr fd;k tk,xkμ
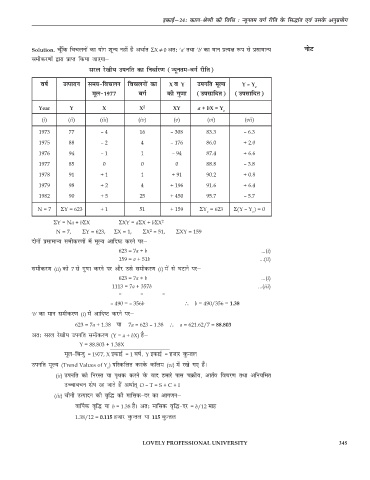
ljy js[kh; miufr dk fuèkkZj.k (U;wure&oxZ jhfr)

o"kZ mRiknu le;&fopyu fopyuksa dk X o Y miufr ewY; Y – Y c
ewy&1977 oxZ dh xq.kk (milkfnr) (milkfnr)

Year Y X X 2 XY a + bX = Y
c
(i) (ii) (iii) (iv) (v) (vi) (vii)
1973 77 – 4 16 – 308 83.3 – 6.3

1975 88 – 2 4 – 176 86.0 + 2.0
1976 94 – 1 1 – 94 87.4 + 6.6
1977 85 0 0 0 88.8 – 3.8
1978 91 + 1 1 + 91 90.2 + 0.8

1979 98 + 2 4 + 196 91.6 + 6.4
1982 90 + 5 25 + 450 95.7 – 5.7
N = 7 ΣY = 623 + 1 51 + 159 ΣY = 623 Σ(Y – Y ) = 0
c
c
ΣY = Na + bΣX ΣXY = aΣX + bΣX 2
2
N = 7, ΣY = 623, ΣX = 1, ΣX = 51, ΣXY = 159
nksuksa izlkekU; lehdj.kksa esa ewY; vkfn"V djus ijμ
623 = 7a + b ...(i)
159 = a + 51b ...(ii)
lehdj.k (ii) dks 7 ls xq.kk djus ij vkSj mls lehdj.k (i) esa ls ?kVkus ijμ
623 = 7a + b ...(i)
1113 = 7a + 357b ...(iii)
– – –
– 490 = – 356b ∴ b = 490/356 = 1.38
‘b’ dk eku lehdj.k (i) esa vkfn"V djus ijμ

623 = 7a + 1.38 ;k 7a = 623 – 1.38 ∴ a = 621.62/7 = 88.803
vr% ljy js[kh; miufr lehdj.k (Y = a + bX) gSμ
Y = 88.803 + 1.38X

ewy&fcUnq = 1977, X bdkbZ = 1 o"kZ] Y bdkbZ = gtkj oqQUry
miufr ewY; (Trend Values of Y ) ifjdfyr djosQ dkWye (vi) esa j[ks x, gSaA
c
(ii) miufr dks fujLr ;k i`Fkd djus osQ ckn gekjs ikl pØh;] vkrZo fopj.k rFkk vfu;fer
mPpkopu 'ks"k jg tkrs gSa vFkkZr~ O – T = S + C + I
(iii) phuh mRiknu dh o`f¼ dh ekfld&nj dk vkx.kuμ
ok£"kd o`f¼ ;k b = 1.38 gSA vr% ekfld o`f¼&nj = b/12 ekg

1.38/12 = 0.115 gtkj oqQUry ;k 115 oqQUry

LOVELY PROFESSIONAL UNIVERSITY 345