Page 200 - DMTH401_REAL ANALYSIS

Real Analysis

Notes
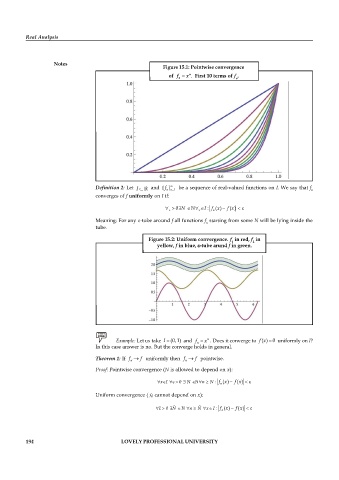
Figure 15.1: Pointwise convergence
of f = x n . First 10 terms of f .
n n

Definition 2: Let I  and { }f n n ¥ = 1 be a sequence of real-valued functions on I. We say that f n
converges of f uniformly on I if:

x
x
" > 0$N Î " ÎI : f ( ) - f ( ) < e
e x n
Meaning: For any e-tube around f all functions f starting from some N will be lying inside the
n
tube.
Figure 15.2: Uniform convergence. f in red, f in
1 2
yellow, f in blue, e-tube arund f in green.

n
Example: Let us take =I (0,1) and f = x . Does it converge to ( ) 0=f x uniformly on I?
n
In this case answer is no. But the converge holds in general.
Theorem 1: If f n  f uniformly then f n  f pointwise.
Proof: Pointwise convergence (N is allowed to depend on x):

x
n
x
I
x
" Î "e > 0 $ N Î " ³ N : f ( ) - f ( ) < e
n
Uniform convergence (  cannot depend on x):
N
 
x
x
x
"e  > 0 $N Î  " ³ N " Î : I f ( ) - f ( ) < e
n
n
194 LOVELY PROFESSIONAL UNIVERSITY