Page 203 - DMTH401_REAL ANALYSIS

Unit 15: Uniform Convergence of Functions

Notes
¥
}
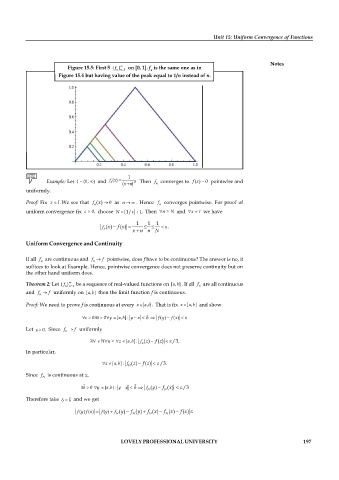
Figure 15.5: First 5 { f n n = 1 on [0, 1]. f is the same one as in
n
Figure 15.4 but having value of the peak equal to 1/n instead of n.

1
.
x
Example: Let =I (0, ¥ and f n ( )= 2 Then f converges to ( ) =f x 0 pointwise and
)
( + n ) n
x
uniformly.
Proof: Fix x Î . I We see that f n ( )  0 as n  ¥ . Hence f converges pointwise. For proof of
x
n
x
e
+
uniform convergence fix e > 0, choose N = [1/ ] 1. Then " ³n N and " Î I we have
1 1 1
x
x
f ( ) - f ( ) = £ £ < . e
n
x + n n N
Uniform Convergence and Continuity
If all f are continuous and f n  f pointwise, does f have to be continuous? The answer is no, it
n
suffices to look at Example. Hence, pointwise convergence does not preserve continuity but on
the other hand uniform does.
Theorem 2: Let { f } ¥ be a sequence of real-valued functions on [ , ]a b . If all f are all continuous
n n = 1 n
and f n  f uniformly on [ , ]a b then the limit function f is continuous.
b
b
a
Proof: We need to prove f is continuous at every Îx a , . That is fix Îx [ , ] and show
a
y
x
"e > 0$d > 0" Î [ , ] : y - x < d Þ f ( ) - f ( ) < e
y
b
Let e > 0. Since f n  f uniformly
z
z
a
n
$N Î " ³ " Î [ , ] : f n ( )- f ( ) < e /3.
b
z
In particular,
z
z
z
" Î [ , ] : f N ( )- f ( ) < e /3.
b
a
Since f is continuous at x,
N
 
y
x
b
a
y
$d > 0 " Î [ , ] : y - x < d Þ f ( )- f ( ) < e /3
N N

Therefore take d = d and we get
y
x
y
x
x
y
f ( ) ( ) = f ( ) + f ( )- f ( )+ f ( )- f ( )- f ( ) £
y
x
f
N N N N
LOVELY PROFESSIONAL UNIVERSITY 197