Page 201 - DMTH401_REAL ANALYSIS

Unit 15: Uniform Convergence of Functions


Hence, for any given e > in pointwise definition it suffices to take N = N taken from uniform Notes
0
e
definition.
15.2 Testing Pointwise and Uniform Convergence

1. Test the pointwise convergence.
2. If there is no pointwise convergence, there is no uniform convergence.
3. If f converges pointwise to some f test the uniform convergence to f.
n

x
ì 0, ¹ 1
n
x
.
Example: Let =I [0,1], f n ( ) = x We see that f converges pointwise to ( ) = í .
f x
n
x
î 1, = 1
Does it converge uniformly to f on I? the answer is no.
Proof: Negation of uniform convergence is
x
x
x
n
$e > 0"N Î $ ³ N $ Î : I f ( ) - f ( ) ³ e
n
1
.
x
x
Take e = . Then "N Î  we have to find n and x such that f n ( ) - f ( ) ³ e Take =n N . Now we
4
æ 1 ö
want to find x. If we take any x Î , 1 we get
÷
è 4 ø
ç n
1
x
x
x
f ( )- f ( ) = f ( )- f ( ) = x N - 0 = x N ³ = . e
x
n N
4
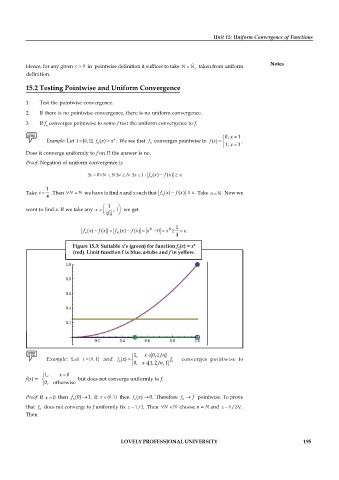
Figure 15.3: Suitable x’s (green) for function f (x) = x 2
2
(red). Limit function f is blue, e-tube and f in yellow.

n
ì 1, x Î [0, 1/ ]
Example: Let I = [0, 1] and f x . f converges pointwise to
( )= í
n
n
n
î 0, x Î [1, 2/ , 1]
ì 1, x = 0
f(x) = í but does not converge uniformly to f.
î 0, otherwise
x
Proof: If =x 0 then f n (0) 1. If x Î (0,1) then f n ( ) 0. Therefore f n  f pointwise. To prove
that f does not converge to f uniformly fix e = 1/2. Then "N Î  choose n = N and x = 1/2 .
N
n
Then

LOVELY PROFESSIONAL UNIVERSITY 195