Page 183 - DMTH504_DIFFERENTIAL_AND_INTEGRAL_EQUATION

Differential and Integral Equation

Notes
= udy dx

n
x
x
y
= u cos( , ) cos( , ) ds ...(6)
w here n denotes the direction of the inward drawn normal to the curve .
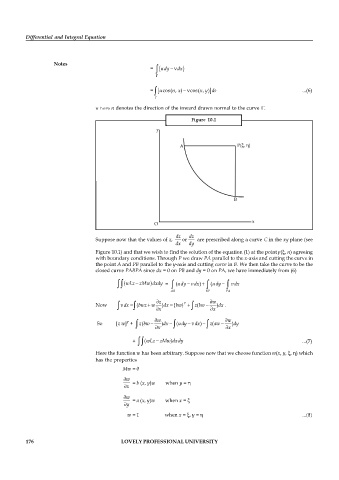
Figure 10.1

dz dz
Suppose now that the values of z, or are prescribed along a curve C in the xy plane (see
dx dy
Figure 10.1) and that we wish to find the solution of the equation (1) at the point p( , n) agreeing
with boundary conditions. Through P we draw PA parallel to the x-axis and cutting the curve in
the point A and PB parallel to the y-axis and cutting curve in B. We then take the curve to be the
closed curve PABPA since dx = 0 on PB and dy = 0 on PA, we have immediately from (6)

wLz zMw dxdy = (udy vdx ) (udy vdx
AB BP PA
z P w
Now vdx (bwz w )dx {bw } ( z bw )dx .
x x
w w
P
So [z w] + z (bw )dx (udy vdx ) ( z aw )dy
x x
+ (wLz zMw )dxdy ...(7)

Here the function w has been arbitrary. Suppose now that we choose function w(x, y, , ) which
has the properties
Mw = 0

w
= b (x, y)w when y =
x
w
= a (x, y)w when x =
y
w = 1 when x = , y =

176 LOVELY PROFESSIONAL UNIVERSITY