Page 216 - DMGT209_QUANTITATIVE_TECHNIQUES_II

Unit 10: Correlation

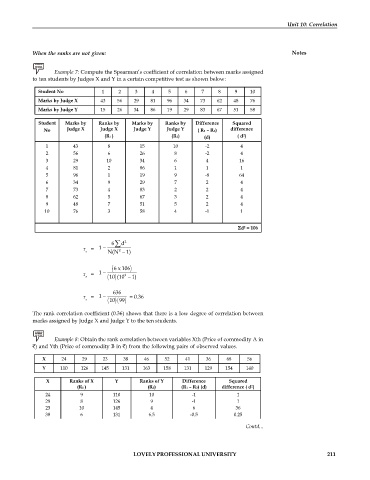
When the ranks are not given: Notes

Example 7: Compute the Spearman’s coefficient of correlation between marks assigned
to ten students by Judges X and Y in a certain competitive test as shown below:
Student No 1 2 3 4 5 6 7 8 9 10
Marks by Judge X 43 56 29 81 96 34 73 62 48 76
Marks by Judge Y 15 26 34 86 19 29 83 67 51 58

Student Marks by Ranks by Marks by Ranks by Difference Squared
No Judge X Judge X Judge Y Judge Y ( R1 – R2) difference
(R1 ) (R2) (d) ( d )
2
1 43 8 15 10 -2 4
2 56 6 26 8 -2 4
3 29 10 34 6 4 16
4 81 2 86 1 1 1
5 96 1 19 9 -8 64
6 34 9 29 7 2 4
7 73 4 83 2 2 4
8 62 5 67 3 2 4
9 48 7 51 5 2 4
10 76 3 58 4 -1 1

2
d = 106

6  d 2
r = 1 
2
s N(N  1)
6 x 106 
r = 1  2
10
s  (10  1)
636
r = 1  = 0.36
10 99
s   
The rank correlation coefficient (0.36) shows that there is a low degree of correlation between
marks assigned by Judge X and Judge Y to the ten students.

Example 8: Obtain the rank correlation between variables Xth (Price of commodity A in
) and Yth (Price of commodity B in ) from the following pairs of observed values.

X 24 29 23 38 46 52 41 36 68 56
Y 110 126 145 131 163 158 131 129 154 140

X Ranks of X Y Ranks of Y Difference Squared
2
(R1 ) (R2) (R1 – R2) (d) difference ( d )
24 9 110 10 -1 1
29 8 126 9 -1 1
23 10 145 4 6 36
38 6 131 6.5 -0.5 0.25
46 4 163 1 3 9
52 3 158 2 1 1 Contd...
41 5 131 6.5 -1.5 2.25
36 7 129 8 -1 1
68 1 154 3 -2 4
-3
5
56 2 140 LOVELY PROFESSIONAL UNIVERSITY9 211

d = 64.5
2