Page 215 - DMGT209_QUANTITATIVE_TECHNIQUES_II

Quantitative Techniques-II

Notes (iv) In the second case,1 when the ranks are not given, when the actual data are given, we have
to assign ranks. We may do so by taking highest value as 1 or the lowest value as 1. When
the two observations are same, then the normal practice is to assign an average rank to the
two observations.

When the ranks are given:

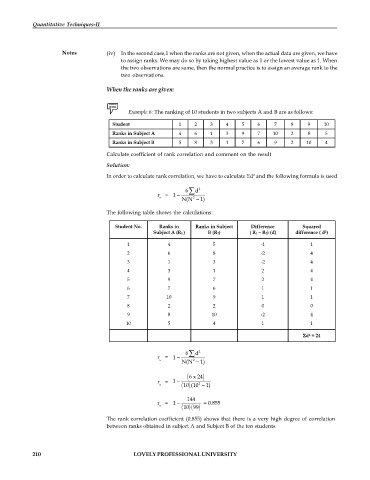
Example 6: The ranking of 10 students in two subjects A and B are as follows:
Student 1 2 3 4 5 6 7 8 9 10
Ranks in Subject A 4 6 1 3 9 7 10 2 8 5
Ranks in Subject B 5 8 3 1 7 6 9 2 10 4
Calculate coefficient of rank correlation and comment on the result

Solution:
2
In order to calculate rank correlation, we have to calculate d and the following formula is used
6  d 2
r = 1 
s 2
N(N  1)
The following table shows the calculations:

Student No. Ranks in Ranks in Subject Difference Squared
Subject A (R1 ) B (R2) ( R1 – R2) (d) difference ( d )
2
1 4 5 -1 1
2 6 8 -2 4
3 1 3 -2 4
4 3 1 2 4
5 9 7 2 4
6 7 6 1 1
7 10 9 1 1
8 2 2 0 0
9 8 10 -2 4
10 5 4 1 1

d = 24
2

6  d 2
r = 1 
s 2
N(N  1)
6 x 24 
r = 1 
2
s  (10  1)
10
144
r = 1  = 0.855
s   
10 99
The rank correlation coefficient (0.855) shows that there is a very high degree of correlation
between ranks obtained in subject A and Subject B of the ten students.

210 LOVELY PROFESSIONAL UNIVERSITY