Page 213 - DMGT209_QUANTITATIVE_TECHNIQUES_II

Quantitative Techniques-II

Notes Correlation of Grouped Data

When the number of observations is large, the data are often classified into two-way frequency
distribution i.e. table where in the values of one variable (X) are represented in the rows while
other variable (Y) in columns. These values can be either discrete or continuous. The frequencies
in each class are shown in cells in the body of the table.
Steps for calculating correlation coefficient for grouped data:
(i) Record the mid-points (mp) of the class intervals for both X and Y variables.

(ii) Choose an assumed mean in X series and calculate the deviations (dx) from it. The same
procedure to be used for Y series and calculate the deviations (dy).
(iii) To simplify the calculations, step deviations can be taken by dividing deviations by a
common factor.
2
(iv) Calculate f.dx, f .dx.dx i.e.f.dx , f.dx.dy for X series and f.dy, f .dy.dy i.e.f.dy , f.dx.dy for Y
2
series.
(v) Substitute all the values obtained in the following formula:


n fdxdy   fdx  fdy
 =
2
2

 fdy

n fdx  
  2  fdx   n fdy    2 
   
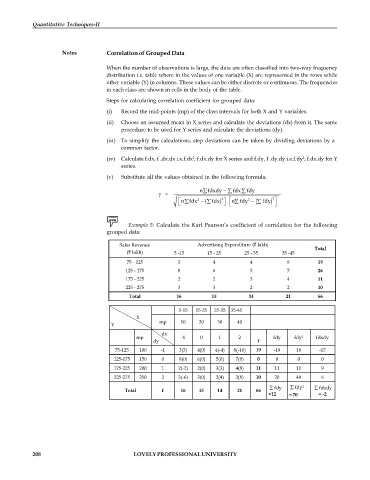
Example 5: Calculate the Karl Pearson’s coefficient of correlation for the following
grouped data:
Sales Revenue Advertising Expenditure ( lakh)
Total
( lakh) 5 -15 15 - 25 25 - 35 35 -45
75 - 125 3 4 4 8 19
125 - 175 8 6 5 7 26
175 - 225 2 2 3 4 11
225 - 275 3 3 2 2 10
Total 16 15 14 21 66

5-15 15-25 25-35 35-45
X
mp 10 20 30 40
Y
dx
mp -1 0 1 2 fdy fdy 2 fdxdy
dy f
75-125 100 -1 3(3) 4(0) 4(-4) 8(-16) 19 -19 19 -17
125-175 150 0 8(0) 6(0) 5(0) 7(0) 0 0 0 0
175-225 200 1 2(-2) 2(0) 3(3) 4(8) 11 11 11 9
225-275 250 2 3(-6) 3(0) 2(4) 2(8) 10 20 40 6

 fdy  fdy 2  fdxdy
Total f 16 15 14 21 66
=12 = 70 = -2

208 LOVELY PROFESSIONAL UNIVERSITY