Page 209 - DMGT404 RESEARCH_METHODOLOGY
P. 209
Unit 10: Time Series
This creates a complex situation in time series analysis. Each factor must be quantified and its Notes
effect ascertained upon product sales. Let us see how this is done. The long-term trend effect T is
reflected in the slope b of the regression equation. We already know how b is calculated even
though minor modifications of the decision formulas will be encountered soon. The quantification
of the cyclical component C is beyond the scope of this book. However, since business cycles
always proceed from peak to trough to new peak and so on, their positive and negative effects
upon a product’s sales cancel out in the long-run. Hence in managerial, as opposed to economic,
decision making, the sum effect of the business cycles may be set equal to zero. This eliminates
the C factor from the equation. Seasonality, if present, is something that must be taken into
consideration because it is a product-inherent variable and therefore it is under the immediate
control of the decision maker. We will quantify the S component and keep it in the equation.
Finally, there are the irregular variations. Do we know in July whether the weather will be
sunny and mild during the four weeks before Diwali? We don’t, but we know that if this
happens, Diwali sales will be severely impacted. Can we forecast such horrible weather
conditions? Not really. We cannot forecast them because they cannot be quantified—a rather
unpleasant characteristic they share with all other type of irregular variations like strikes,
earthquakes, power failure, etc. Yet, something strange usually happens after such an irregular
variation from “normal” has occurred. Whatever people did not do because of it, like not
buying a product, they attempt to catch up with quickly. Therefore the factor effect may also be
assumed to cancel out over time and it may be dropped from the equation which then appears
to the manager as TS = T + S.
Linear Analysis
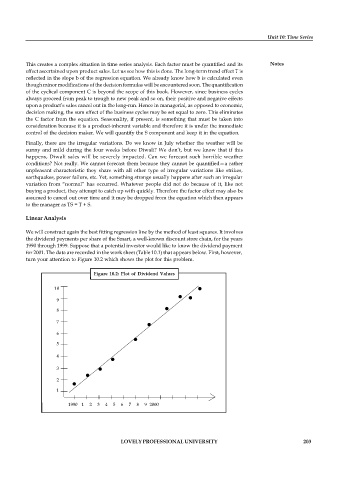
We will construct again the best fitting regression line by the method of least squares. It involves
the dividend payments per share of the Smart, a well-known discount store chain, for the years
1990 through 1999. Suppose that a potential investor would like to know the dividend payment
for 2001. The data are recorded in the work sheet (Table 10.1) that appears below. First, however,
turn your attention to Figure 10.2 which shows the plot for this problem.
Figure 10.2: Plot of Dividend Values
10
9
8
7
6
5
4
3
2
1
1990 1 2 3 4 5 6 7 8 9 2000
LOVELY PROFESSIONAL UNIVERSITY 203