Page 210 - DMGT404 RESEARCH_METHODOLOGY

Research Methodology

Notes Think for a moment about the qualitative nature of the time variable. It is expressed in years in
this case but could be quarters, months, days, hours, minutes or any other time measurement
unit. How does it differ from advertising expenditures, the independent variable that we examine
in the preceding section? Is there a difference in the effect that a unit of each has on the dependent
variable, or, 1 million in one case and 1 year in the other? Time, as you can readily see is
constant. One year has the same effects as any other. This is not true for advertising expenditures,
especially when you leave the linear environment and enter the nonlinear environments. Then
there may be qualitative difference in the sales impact as advertising expenditures are increased
or decreased by unit.
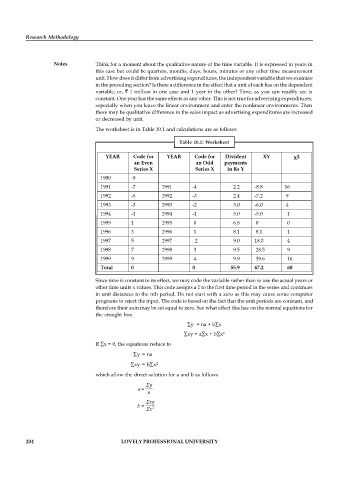
The worksheet is in Table 10.1 and calculations are as follows:

Table 10.1: Worksheet

YEAR Code for YEAR Code for Divident XY X
2
an Even an Odd payments
Series X Series X in Rs Y
1990 -9
1991 -7 1991 -4 2.2 -8.8 16
1992 -5 1992 -3 2.4 -7.2 9
1993 -3 1993 -2 3.0 -6.0 4
1994 -1 1994 -1 5.0 -5.0 1
1995 1 1995 0 6.8 0 0
1996 3 1996 1 8.1 8.1 1
1997 5 1997 2 9.0 18.0 4
1998 7 1998 3 9.5 28.5 9
1999 9 1999 4 9.9 39.6 16
Total 0 0 55.9 67.2 60

Since time is constant in its effect, we may code the variable rather than to use the actual years or
other time units x values. This code assigns a 1 to the first time period in the series and continues
in unit distances to the nth period. Do not start with a zero as this may cause some computer
programs to reject the input. The code is based on the fact that the unit periods are constant, and
therefore their sum may be set equal to zero. See what effect this has on the normal equations for
the straight line.

y = na + bx
xy = ax + bx 2
If x = 0, the equations reduce to
y = na

xy = bx 2
which allow the direct solution for a and b as follows
S y
a =
n
S xy
b =
S x 2

204 LOVELY PROFESSIONAL UNIVERSITY