Page 327 - DCOM504_SECURITY_ANALYSIS_AND_PORTFOLIO_MANAGEMENT

Security Analysis and Portfolio Management

Notes The Treynor measure only measures systematic risk – it automatically assumes an adequately
diversified portfolio.
You can compare the T measures for different portfolios. The higher the T value, the better the
portfolio performance. For instance, the T value for the market is:
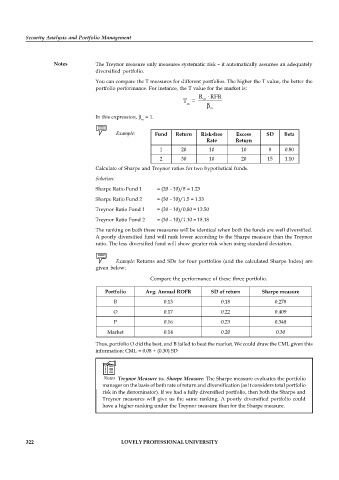
R RFR
T = m
m
m
In this expression, = 1.
m

Example: Fund Return Risk-free Excess SD Beta
Rate Return
1 20 10 10 8 0.80
2 30 10 20 15 1.10

Calculate of Sharpe and Treynor ratios for two hypothetical funds.
Solution:
Sharpe Ratio Fund 1 = (20 – 10)/8 = 1.23
Sharpe Ratio Fund 2 = (30 – 10)/1.5 = 1.33

Treynor Ratio Fund 1 = (20 – 10)/0.80 = 12.50
Treynor Ratio Fund 2 = (30 – 10)/1.10 = 18.18
The ranking on both these measures will be identical when both the funds are well diversified.
A poorly diversified fund will rank lower according to the Sharpe measure than the Treynor
ratio. The less diversified fund will show greater risk when using standard deviation.

Example: Returns and SDs for four portfolios (and the calculated Sharpe Index) are
given below:

Compare the performance of these three portfolio.

Portfolio Avg. Annual ROFR SD of return Sharpe measure
B 0.13 0.18 0.278
O 0.17 0.22 0.409
P 0.16 0.23 0.348
Market 0.14 0.20 0.30

Thus, portfolio O did the best, and B failed to beat the market. We could draw the CML given this
information: CML = 0.08 + (0.30) SD

Notes Treynor Measure vs. Sharpe Measure: The Sharpe measure evaluates the portfolio
manager on the basis of both rate of return and diversification (as it considers total portfolio
risk in the denominator). If we had a fully diversified portfolio, then both the Sharpe and
Treynor measures will give us the same ranking. A poorly diversified portfolio could
have a higher ranking under the Treynor measure than for the Sharpe measure.

322 LOVELY PROFESSIONAL UNIVERSITY