Page 190 - DMTH201_Basic Mathematics-1

Unit 6: Functions

Notes
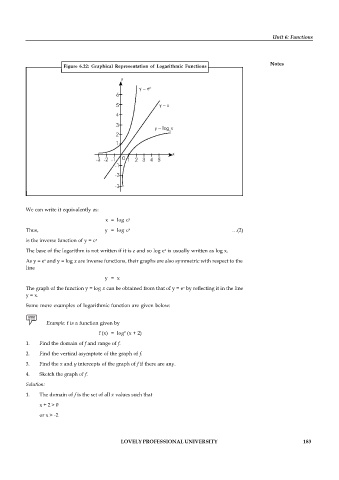
Figure 6.22: Graphical Representation of Logarithmic Functions

We can write it equivalently as:
x = log e y
Thus, y = log e x …(2)
is the inverse function of y = e x
x
The base of the logarithm is not written if it is e and so log e is usually written as log x.
As y = e and y = log x are inverse functions, their graphs are also symmetric with respect to the
x
line
y = x

x
The graph of the function y = log x can be obtained from that of y = e by reflecting it in the line
y = x.
Some more examples of logarithmic function are given below:

Example: f is a function given by
f (x) = log (x + 2)
2
1. Find the domain of f and range of f.
2. Find the vertical asymptote of the graph of f.
3. Find the x and y intercepts of the graph of f if there are any.

4. Sketch the graph of f.
Solution:
1. The domain of f is the set of all x values such that
x + 2 > 0
or x > -2

LOVELY PROFESSIONAL UNIVERSITY 183