Page 216 - DMGT524_TOTAL_QUALITY_MANAGEMENT

Unit 14: Statistical Process Control

Limit (LCL), are also shown on the chart. These control limits are chosen so that almost all of the Notes
data points will fall within these limits as long as the process remains in-control.

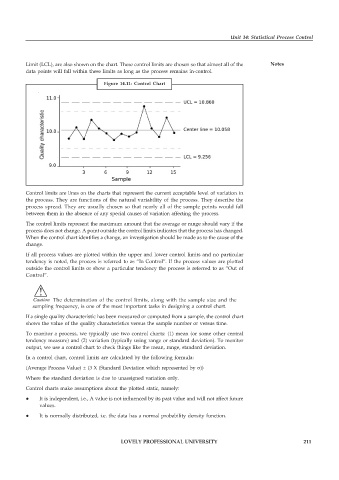
Figure 14.11: Control Chart

Control limits are lines on the charts that represent the current acceptable level of variation in
the process. They are functions of the natural variability of the process. They describe the
process spread. They are usually chosen so that nearly all of the sample points would fall
between them in the absence of any special causes of variation affecting the process.

The control limits represent the maximum amount that the average or range should vary if the
process does not change. A point outside the control limits indicates that the process has changed.
When the control chart identifies a change, an investigation should be made as to the cause of the
change.
If all process values are plotted within the upper and lower control limits and no particular
tendency is noted, the process is referred to as “In Control”. If the process values are plotted
outside the control limits or show a particular tendency the process is referred to as “Out of
Control”.

!
Caution The determination of the control limits, along with the sample size and the
sampling frequency, is one of the most important tasks in designing a control chart.
If a single quality characteristic has been measured or computed from a sample, the control chart
shows the value of the quality characteristics versus the sample number or versus time.

To monitor a process, we typically use two control charts: (1) mean (or some other central
tendency measure) and (2) variation (typically using range or standard deviation). To monitor
output, we use a control chart to check things like the mean, range, standard deviation.
In a control chart, control limits are calculated by the following formula:
(Average Process Value) ± (3 X (Standard Deviation which represented by σ))
Where the standard deviation is due to unassigned variation only.

Control charts make assumptions about the plotted static, namely:
It is independent, i.e., A value is not influenced by its past value and will not affect future
values.

It is normally distributed, i.e. the data has a normal probability density function.

LOVELY PROFESSIONAL UNIVERSITY 211