Page 141 - DLIS401_METHODOLOGY_OF_RESEARCH_AND_STATISTICAL_TECHNIQUES

Methodology of Research and Statistical Techniques

Notes 9.3.3 Frequency Polygon

For plotting a frequency polygon, as in case of histogram, the values of the variable are taken
on the horizontal axis of the graph and the frequencies are taken on the vertical axis of the
graph. In the case of a frequency polygon, one has to indicate the mid points of the C.I. on
the horizontal axis, instead of indicating the boundaries of the interval, Here the mid point of
the intervals just before the lowest interval and just after the highest interval are also to be
indicated.
Now by taking the mid points one by one, the points above them are to be plotted corresponding
to the frequencies of the intervals. In case of the two additional mid points, the frequency
being zero, the points to be plotted are on the X-axis itself. The adjoining points so plotted are
to be jained by straight line segments.
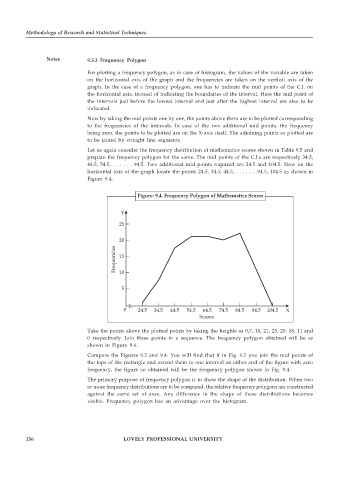
Let us again consider the frequency distribution of mathematics scores shown in Table 9.5 and
prepare the frequency polygon for the same. The mid points of the C.I.s are respectively 34.5,
44.5, 54.5, . . . . . . 94.5. Two additional mid points required are 24.5 and 104.5. Now on the
horizontal axis of the graph locate the points 24.5, 34.5, 44.5, . . . . . . .94.5, 104.5 as shown in
Figure 9.4.

Figure: 9.4. Frequency Polygon of Mathematics Scores

Y

25

20
Frequencies 15

10

5

0 24.5 34.5 44.5 54.5 64.5 74.5 84.5 94.5 104.5 X
Scores

Take the points above the plotted points by taking the heights as 0,7, 18, 21, 25, 20, 18, 11 and
0 respectively. Join these points in a sequence. The frequency polygon obtained will be as
shown in Figure 9.4.
Compare the Figures 9.2 and 9.4. You will find that if in Fig. 9.2 you join the mid points of
the tops of the rectangle and extend them to one interval on either end of the figure with zero
frequency, the figure so obtained will be the frequency polygon shown in Fig. 9.4.
The primary purpose of frequency polygon is to show the shape of the distribution. When two
or more frequency distributions are to be compared, the relative frequency polygons are constructed
against the same set of axes. Any difference in the shape of these distributions becomes
visible. Frequency polygon has an advantage over the histogram.

136 LOVELY PROFESSIONAL UNIVERSITY