Page 176 - DECO504_STATISTICAL_METHODS_IN_ECONOMICS_ENGLISH

Statistical Methods in Economics

Notes (II and III)

∑D 2 = 214, N = 10

6 × 214 1284
= 1 − 3 = −1 = 1 – 1.297 = – 0.297.
10 − 10 990
rd
Rank correlation between the judgments of the 1 and 3 Judge:
st
6D 2
∑
R= −1
N 3 − N
(I and III)
∑D 2 = 60, N = 10

660 360
×
= 1 − = −1 = 1 – .364 = + 0.636
10 3 − 10 990
Thus we find the first and third judges have the nearest approach to common tastes
in beauty.
B. Where Ranks are not Given ?
When we are given the actual data and not the ranks, it will be necessary to assign the ranks.
Ranks can be assigned by taking either the highest value as 1 or the lowest value as 1. But
whether we start with the lowest value or the highest value we must follow the same method in
case of both the variables.
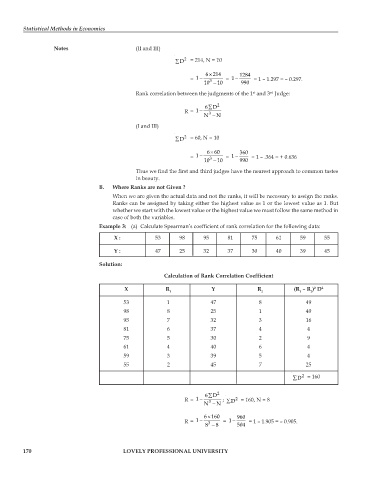
Example 3: (a) Calculate Spearman’s coefficient of rank correlation for the following data:
X : 53 98 95 81 75 61 59 55

Y : 47 25 32 37 30 40 39 45

Solution:
Calculation of Rank Correlation Coefficient

X R Y R (R – R ) D 2
2
1 2 1 2
53 1 47 8 49
98 8 25 1 49
95 7 32 3 16
81 6 37 4 4
75 5 30 2 9
61 4 40 6 4
59 3 39 5 4
55 2 45 7 25

∑D 2 = 160

∑
6D 2
R= −1 ; ∑D = 160, N = 8
2
N 3 − N
×
6160 960
R= 1 − 3 = −1 = 1 – 1.905 = – 0.905.
8 − 8 504

170 LOVELY PROFESSIONAL UNIVERSITY