Page 175 - DECO504_STATISTICAL_METHODS_IN_ECONOMICS_ENGLISH
P. 175
Unit 11: Rank Correlation Method
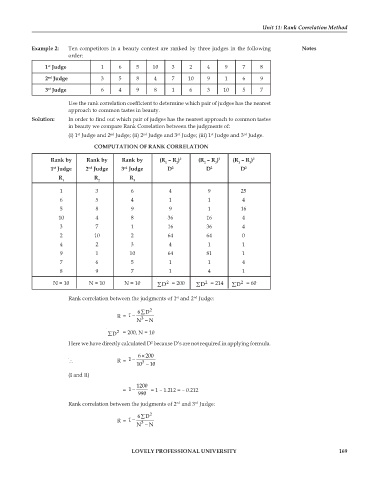
Example 2: Ten competitors in a beauty contest are ranked by three judges in the following Notes
order:
1 Judge 1 6 5 10 3 2 4 9 7 8
st
2 Judge 3 5 8 4 7 10 9 1 6 9
nd
3 Judge 6 4 9 8 1 6 3 10 5 7
rd
Use the rank correlation coefficient to determine which pair of judges has the nearest
approach to common tastes in beauty.
Solution: In order to find out which pair of judges has the nearest approach to common tastes
in beauty we compare Rank Correlation between the judgments of:
(i) 1 Judge and 2 Judge; (ii) 2 Judge and 3 Judge; (iii) 1 Judge and 3 Judge.
st
rd
nd
st
nd
rd
COMPUTATION OF RANK CORRELATION
Rank by Rank by Rank by (R – R ) 2 (R – R ) 2 (R – R ) 2
1 2 2 3 1 3
1 Judge 2 Judge 3 Judge D 2 D 2 D 2
nd
rd
st
R R R
1 2 3
1 3 6 4 9 25
6 5 4 1 1 4
5 8 9 9 1 16
10 4 8 36 16 4
3 7 1 16 36 4
2 10 2 64 64 0
4 2 3 4 1 1
9 1 10 64 81 1
7 6 5 1 1 4
8 9 7 1 4 1
N = 10 N = 10 N = 10 ∑D 2 = 200 ∑D 2 = 214 ∑D 2 = 60
Rank correlation between the judgments of 1 and 2 Judge:
nd
st
6D 2
∑
R= −1
N 3 − N
∑D 2 = 200, N = 10
Here we have directly calculated D because D’s are not required in applying formula.
2
6 × 200
∴ R= 1 −
10 3 − 10
(I and II)
1200
= −1 = 1 – 1.212 = – 0.212
990
Rank correlation between the judgments of 2 and 3 Judge:
nd
rd
∑
6D 2
R= −1
N 3 − N
LOVELY PROFESSIONAL UNIVERSITY 169