Page 253 - DECO504_STATISTICAL_METHODS_IN_ECONOMICS_ENGLISH

Unit 19: Methods—Weighted Average of Price Relatives

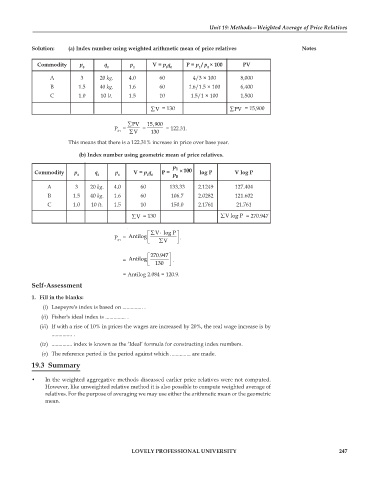
Solution: (a) Index number using weighted arithmetic mean of price relatives Notes

Commodity p q p V = p q P = p / p × 100 PV
0 0 1 0 0 1 0
A 3 20 kg. 4.0 60 4/3 × 100 8,000
B 1.5 40 kg. 1.6 60 1.6/1.5 × 100 6,400
C 1.0 10 lt. 1.5 10 1.5/1 × 100 1,500

∑ V = 130 ∑ PV = 15,900

∑ PV 15,900
P = = = 122.31.
01 ∑ V 130
This means that there is a 122.31% increase in price over base year.
(b) Index number using geometric mean of price relatives.

p 1
Commodity p q p V = p q P = × 100 log P V log P
0 0 1 0 0 p 0
A 3 20 kg. 4.0 60 133.33 2.1249 127.404
B 1.5 40 kg. 1.6 60 106.7 2.0282 121.602
C 1.0 10 lt. 1.5 10 150.0 2.1761 21.761
∑ V = 130 ∑ V log P = 270.947

∑ ⎡ V log P ⎤ ⋅
P = Antilog ⎢ ⎥ .
01 ⎣ ∑ V ⎦

⎡ 270.947 ⎤
= Antilog ⎢ ⎣ 130 ⎥ ⎦ .

= Antilog 2.084 = 120.9.
Self-Assessment

1. Fill in the blanks:
(i) Laepeyre's index is based on ............... .
(ii) Fisher's ideal index is ............... .
(iii) If with a rise of 10% in prices the wages are increased by 20%, the real wage increase is by
............... .
(iv) ............... index is known as the ‘Ideal’ formula for constructing index numbers.
(v) The reference period is the period against which ............... are made.
19.3 Summary

• In the weighted aggregative methods discussed earlier price relatives were not computed.
However, like unweighted relative method it is also possible to compute weighted average of
relatives. For the purpose of averaging we may use either the arithmetic mean or the geometric
mean.

LOVELY PROFESSIONAL UNIVERSITY 247