Page 142 - DECO504_STATISTICAL_METHODS_IN_ECONOMICS_HINDI

vFkZ'kkL=k esa lkaf[;dh; fof/;k¡

uksV 7 64 48
8 72 50
9 56 62
10 58 60
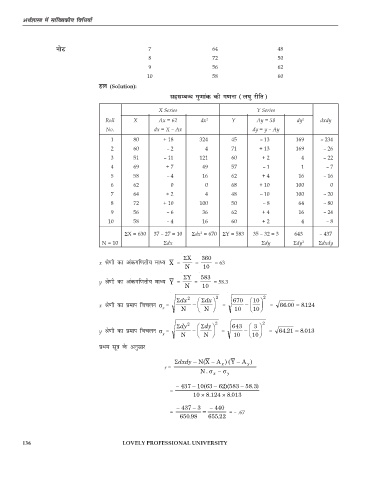
gy (Solution):

lglEcU/ xq.kkad dh x.kuk (y?kq jhfr)
X Series Y Series
Roll X Ax = 62 dx 2 Y Ay = 58 dy 2 dxdy
No. dx = X – Ax dy = y – Ay
1 80 + 18 324 45 – 13 169 – 234
2 60 – 2 4 71 + 13 169 – 26
3 51 – 11 121 60 + 2 4 – 22
4 69 + 7 49 57 – 1 1 – 7
5 58 – 4 16 62 + 4 16 – 16
6 62 0 0 68 + 10 100 0
7 64 + 2 4 48 – 10 100 – 20
8 72 + 10 100 50 – 8 64 – 80
9 56 – 6 36 62 + 4 16 – 24
10 58 – 4 16 60 + 2 4 – 8

ΣX = 630 37 – 27 = 10 Σdx = 670 ΣY = 583 35 – 32 = 3 643 – 437
2
N = 10 Σdx Σdy Σdy 2 Σdxdy
ΣX 360
x Js.kh dk vadxf.krh; ekè; X = = = 63
N 10
ΣY 583
y Js.kh dk vadxf.krh; ekè; Y = = = 58.3
N 10
Σ 2 −G Σdx F dxI J 2 670 F 10I 2
−G J
.
x Js.kh dk izeki fopyu σ = N H N K = 10 H 10K = 66 00. = 8124
x
Σ 2 Σdy F dyI 2 643 F I 2
3
−G
−G J
.
y Js.kh dk izeki fopyu σ = N H N K J = 10 H 10K = 64 21. = 8 013
y
izFke lw=k osQ vuqlkj
Σdxdy –N(X − A )( Y − A )
r = x y
N . σ x − σ y

− − 437 − 10(63 62)( − 583 58.3 )
=
.
10 × . × 8 124 8 013
− − 437 3 − 440
= = = – .67
650 98 655 22
.
.

136 LOVELY PROFESSIONAL UNIVERSITY