Page 152 - DECO504_STATISTICAL_METHODS_IN_ECONOMICS_HINDI

vFkZ'kkL=k esa lkaf[;dh; fof/;k¡

uksV U;wure oxZ jhfr }kjk Kkr lglEcUèk xq.kkad dk fpÉ ogh gksxk tks b vpj ewy; dk gksrk gSA
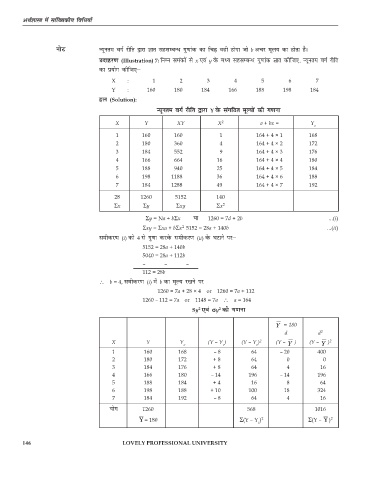
mnkgj.k (Illustration) 7: fuEu leadksa ls x ,oa y osQ eè; lglEcUèk xq.kkad Kkr dhft,] U;wure oxZ jhfr
dk iz;ksx dhft,μ
X : 1 2 3 4 5 6 7
Y : 160 180 184 166 188 198 184
gy (Solution):
U;wure oxZ jhfr }kjk Y osQ laxfBr ewY;ksa dh x.kuk

X Y XY X 2 a + bx = Y c
1 160 160 1 164 + 4 × 1 168
2 180 360 4 164 + 4 × 2 172
3 184 552 9 164 + 4 × 3 176
4 166 664 16 164 + 4 × 4 180
5 188 940 25 164 + 4 × 5 184
6 198 1188 36 164 + 4 × 6 188
7 184 1288 49 164 + 4 × 7 192
28 1260 5152 140
Σx Σy Σxy Σx 2
Σy = Na + bΣx ;k 1260 = 7d + 2b ...(i)
2
Σxy = Σxa + bΣx 5152 = 28a + 140b ...(ii)
lehdj.k (i) dks 4 ls xq.kk djosQ lehdj.k (ii) osQ ?kVkus ijμ
5152 = 28a + 140b
5040 = 28a + 112b
– – –
112 = 28b
∴ b = 4, lehdj.k (i) eas b dk ewY; j[kus ij
1260 = 7a + 28 × 4 or 1260 = 7a + 112
1260 – 112 = 7a or 1148 = 7a ∴ a = 164
2
2
Sy ,oa σσ σσ σy dh x.kuk
Y = 180
d d 2
X Y Y c (Y – Y ) (Y – Y ) 2 (Y – Y ) (Y – Y ) 2
c
c
1 160 168 – 8 64 – 20 400
2 180 172 + 8 64 0 0
3 184 176 + 8 64 4 16
4 166 180 – 14 196 – 14 196
5 188 184 + 4 16 8 64
6 198 188 + 10 100 18 324
7 184 192 – 8 64 4 16

;ksx 1260 568 1016
Y = 180 Σ(Y – Y ) 2 Σ(Y – Y ) 2
c

146 LOVELY PROFESSIONAL UNIVERSITY