Page 183 - DECO504_STATISTICAL_METHODS_IN_ECONOMICS_HINDI

bdkbZ—11% dksfV lglaca/ fof/

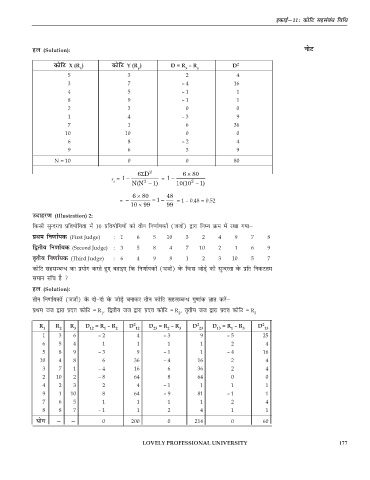
gy (Solution): uksV

dksfV X (R ) dksfV Y (R ) D = R – R y D 2
x
x
y
5 3 2 4
3 7 – 4 16
4 5 – 1 1
8 9 – 1 1
2 2 0 0
1 4 – 3 9
7 1 6 36
10 10 0 0
6 8 – 2 4
9 6 3 9
N = 10 0 0 80

6ΣD 2 6 × 80
r = 1 − = 1 −
2
(
s N(N 2 − 1) 10 10 − 1)
6 × 80 48
= − =− = 1 – 0.48 = 0.52
1
10 × 99 99
mnkgj.k (Illustration) 2:
fdlh lqUnjrk izfr;ksfxrk esa 10 izfr;ksfx;ksa dks rhu fu.kkZ;dksa (ttksa) }kjk fuEu Øe esa j[kk x;kμ
izFke fu.kkZ;d (First Judge) : 1 6 5 10 3 2 4 9 7 8
f}rh; fu.kkZ;d (Second Judge) : 3 5 8 4 7 10 2 1 6 9

r`rh; fu.kkZ;d (Third Judge) : 6 4 9 8 1 2 3 10 5 7
dksfV lglEcU/ dk iz;ksx djrs gq, crkb, fd fu.kkZ;dksa (ttksa) osQ fdl tksM+s dh lqUnjrk osQ izfr fudVre
leku #fp gS \
gy (Solution):

rhu fu.kkZ;dksa (ttksa) osQ nks&nks osQ tksM+s cukdj rhu dksfV lglEcU/ xq.kkad Kkr djsaμ
izFke tt }kjk iznÙk dksfV = R , f}rh; tt }kjk iznÙk dksfV = R , r`rh; tt }kjk iznÙk dksfV = R
1 2 3
R 1 R 2 R 3 D = R – R 2 D 2 12 D = R – R 3 D 2 23 D = R – R 3 D 2 13
1
2
23
13
1
12
1 3 6 – 2 4 – 3 9 – 5 25
6 5 4 1 1 1 1 2 4
5 8 9 – 3 9 – 1 1 – 4 16
10 4 8 6 36 – 4 16 2 4
3 7 1 – 4 16 6 36 2 4
2 10 2 – 8 64 8 64 0 0
4 2 3 2 4 – 1 1 1 1
9 1 10 8 64 – 9 81 – 1 1
7 6 5 1 1 1 1 2 4
8 8 7 – 1 1 2 4 1 1
;ksx — — 0 200 0 214 0 60

LOVELY PROFESSIONAL UNIVERSITY 177