Page 184 - DECO504_STATISTICAL_METHODS_IN_ECONOMICS_HINDI

vFkZ'kkL=k esa lkaf[;dh; fof/;k¡

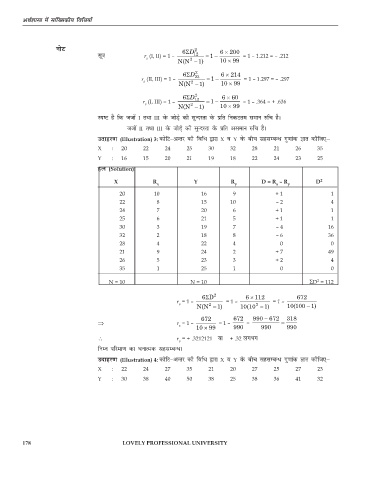
uksV 6ΣD 2 6 × 200
1
lw=k r (I, II) = 1 – 12 =− = 1 – 1.212 = – .212
s
2
N(N − 1) 10 × 99
6ΣD 2 6 × 214
1
r (II, III) = 1 – 23 =− = 1 – 1.297 = – .297
s 2
N(N − 1) 10 × 99
6ΣD 2 6 × 60
13
1
r (I, III) = 1 – N(N − 1) =− 10 × 99 = 1 – .364 = + .636
2
s
Li"V gS fd ttksa I rFkk III osQ tksM+s dh lqUnjrk osQ izfr fudVre leku #fp gSA
ttksa II rFkk III osQ tksM+s dh lqUnjrk osQ izfr vleku #fp gSA
mnkgj.k (Illustration) 3: dksfV&vUrj dh fof/ }kjk X o Y osQ chp lglEcU/ xq.kkad Kkr dhft,μ
X : 20 22 24 25 30 32 28 21 26 35
Y : 16 15 20 21 19 18 22 24 23 25
gy (Solution):

X R x Y R y D = R – R y D 2
x
20 10 16 9 + 1 1
22 8 15 10 – 2 4
24 7 20 6 + 1 1
25 6 21 5 + 1 1
30 3 19 7 – 4 16
32 2 18 8 – 6 36
28 4 22 4 0 0
21 9 24 2 + 7 49
26 5 23 3 + 2 4
35 1 25 1 0 0
2
N = 10 N = 10 ΣD = 112
×
6ΣD 2 6112 672
r = 1 – N(N − 1) = 1 – 10(10 2 −1) = 1 – 10 100 1)
−
2
s
(
672 672 990 − 672 318
⇒ r = 1 – 10 × 99 = 1 – 990 = 990 = 990
s
∴ r = + .3212121 ;k + .32 yxHkx
s
fuEu ifjek.k dk /ukRed lglEcU/A
mnkgj.k (Illustration) 4: dksfV&vUrj dh fof/ }kjk X o Y osQ chp lglEcU/ xq.kkad Kkr dhft,μ
X : 22 24 27 35 21 20 27 25 27 23

Y : 30 38 40 50 38 25 38 36 41 32

178 LOVELY PROFESSIONAL UNIVERSITY