Page 186 - DECO504_STATISTICAL_METHODS_IN_ECONOMICS_HINDI

vFkZ'kkL=k esa lkaf[;dh; fof/;k¡

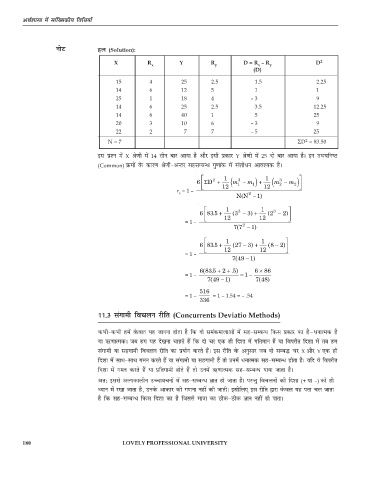
uksV gy (Solution):
X R Y R D = R – R D 2
x y x y
(D)
15 4 25 2.5 1.5 2.25
14 6 12 5 1 1
25 1 18 4 – 3 9
14 6 25 2.5 3.5 12.25
14 6 40 1 5 25
20 3 10 6 – 3 9
22 2 7 7 – 5 25
N = 7 ΣD = 83.50
2

bl iz'u esa X Js.kh esa 14 rhu ckj vk;k gS vkSj blh izdkj Y Js.kh esa 25 nks ckj vk;k gSA bu mHk;fu"B
(Common) Øeksa osQ dkj.k Js.kh&vUrj lglEcU/ xq.kkad esa la'kks/u vko';d gSA
L 1 1 O
6 ΣD + M N 2 1 e 3 − m 1j + m m 2 e 3 − m 2 P j Q
r = 1 – 12 12
2
s
N(N − 1)
L 1 1 O
6835 + M N . 3 ( 3 − 3) + 2 ( 3 − 2) P Q
= 1 – 12 12
2
77 − 1)
(
L 1 1 O
6835 + M N . 12 ( 27 3) + − 12 8 ( − 2) P Q
= 1 –
−
(
749 1)
(
+
6835 + . 2 . 5) 6 × 86
1
= 1 – =−
−
(
(
749 1) 748)
516
= 1 – = 1 – 1.54 = – .54
336
11-3 laxkeh fopyu jhfr (Concurrents Deviatio Methods)
dHkh&dHkh gesa osQoy ;g tkuuk gksrk gS fd nks leadekykvksa esa lg&lEcU/ fdl izdkj dk gSμ/ukRed gS
;k ½.kkRedA tc ge ;g ns[kuk pkgrs gSa fd nks pj ,d gh fn'kk esa xfreku gSa ;k foijhr fn'kk esa rc ge
laxkeh ;k lgxkeh fopyu jhfr dk iz;ksx djrs gSaA bl jhfr osQ vuqlkj tc nks lEc¼ pj X vkSj Y ,d gh
fn'kk esa lkFk&lkFk xeu djrs gSa ;k laxkeh ;k lgxkeh gSa rks muesa /ukRed lg&lEcU/ gksrk gSA ;fn os foijhr
fn'kk esa xeu djrs gSa ;k izfrxkeh gksrs gSa rks muesa ½.kkRed lg&lEcU/ ik;k tkrk gSA
vr% blls vYidkyhu mPpkopuksa esa lg&lEcU/ Kkr gks tkrk gSA ijUrq fopyuksa dh fn'kk (+ ;k –) dks gh
è;ku esa j[kk tkrk gS] muosQ vkdkj dh x.kuk ugha dh tkrhA blhfy, bl jhfr }kjk osQoy ;g irk py tkrk
gS fd lg&lEcU/ fdl fn'kk dk gS ftlls ek=kk dk Bhd&Bhd Kku ugha gks ikrkA

180 LOVELY PROFESSIONAL UNIVERSITY