Page 239 - DMTH401_REAL ANALYSIS

Unit 19: Arzelà’s Theorem and Weierstrass Approximation Theorem

2 2 Notes
æ k - nxö (k - nx)
2
|k/n – x|  ç è n ÷ ø    n   1.
2 2
By using this remark in the second sum and by increasing number of summants in the first sum
we get
 n n
×
+
å p (x) 2 f å 1 p (x)
2 k 0 kn sup k: k x-  kn
=
n
 2 f sup n
2
 1 × + å (k - nx) p (x)
2
2 n  2 k: k x-  kn
n
 2 f sup n  2 f sup  2 f sup
-
2
 + å (k - nx) p (x) = + 2 2 nx(1 x)  + 2 .

kn
2
2 n  2 k 0 2 n  2 n
=
 1
2 f sup 
Let N be such that 2 < . Then n"  N and x" Î[0, 1]
N 2
 2 f sup  2 f sup  
f

-
B (x) f(x) < +  + < + = .
n
2 n 2 2 N 2 2 2
Proof: In this proof we shrink our function f to [0, 1], where it can be approximated uniformly by
Bernstein polynomials and then scale these polynomials from [0, 1] to [a, b] where they will
approximate the original function. Define g : [0, 1]  , g(t) = f(x(t)). Where x(t) = a + (b – a)t for
g
t Î [0, 1]. We see that g is continuous since it is a composite of two continuous functions. As B 
n
æ
g g x a- ö
g uniformly. Define q (x) = B (t(x)) = B ç ÷ . Then
b a ø
n n n
è -
g
a - f sup = sup q (x) f(x)- = sup B (t(x)) g(t(x))-
n
n
n
x [a,b] x [a,b]
Î
Î
g
g
= sup B (t) g(t) = B- g n - g  0, since B  g uniformly.
n
n
t [0,1] sup
Î
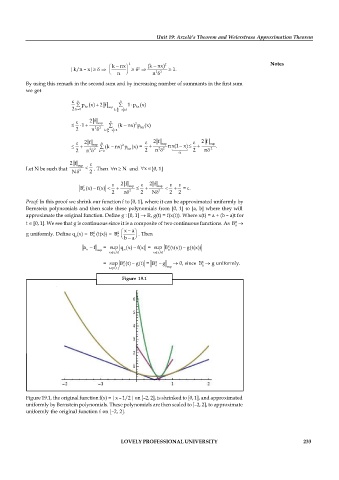
Figure 19.1

Figure 19.1, the original function f(x) = |x – 1/2| on [–2, 2], is shrinked to [0, 1], and approximated
uniformly by Bernstein polynomials. These polynomials are then scaled to [–2, 2], to approximate
uniformly the original function f on [–2, 2].

LOVELY PROFESSIONAL UNIVERSITY 233