Page 241 - DMTH401_REAL ANALYSIS

Unit 19: Arzelà’s Theorem and Weierstrass Approximation Theorem

Notes
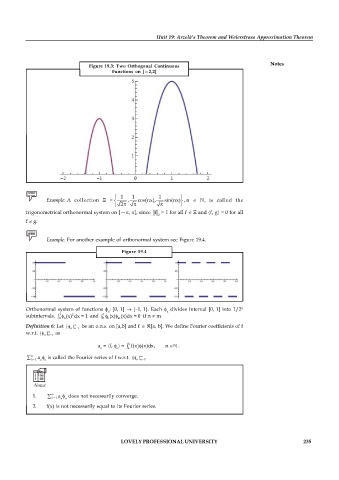
Figure 19.3: Two Orthogonal Continuous
Functions on [—2,2]

ì 1 1 1 ü
Example: A collection  = í , cos(nx), sin(nx) , ý n Î , is called the
î 2p p p þ
trigonometrical orthonormal system on [—p, p], since f = 1 for all f Î  and f, g = 0 for all
2
f ¹ g.

Example: For another example of orthonormal system see Figure 19.4.

Figure 19.4

Orthonormal system of functions f : [0, 1]  {–1, 1}. Each f divides interval [0, 1] into 1/2 n
n n
1
2
1
subintervals. ò f (x) dx = 1 and ò f (x)f (x)dx = 0 if n ¹ m
0 n 0 n m
Definition 6: Let {f } ¥ be an o.n.s. on [a,b] and f Î [a, b]. We define Fourier coefficients of f
n n 1 =
w.r.t. {f } ¥ as
n n 1
=
b
f
a = f, f  = ò f(x) (x)dx, n Î  .
n n a
} .
¥
å ¥ n 1 a f is called the Fourier series of f w.r.t. {f n n 1
=
n n
=
Notes
1. å ¥ n 1 a f does not necessarily converge.
=
n n
2. f(x) is not necessarily equal to its Fourier series.

LOVELY PROFESSIONAL UNIVERSITY 235