Page 261 - DMTH402_COMPLEX_ANALYSIS_AND_DIFFERENTIAL_GEOMETRY

Complex Analysis and Differential Geometry

Notes
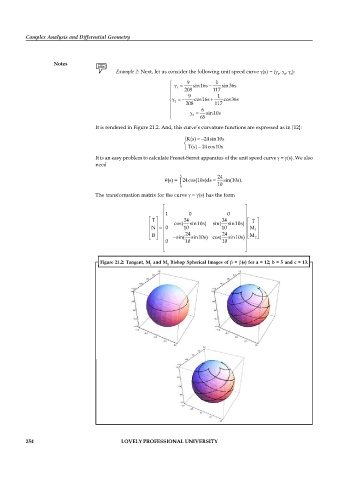
Example 2: Next, let us consider the following unit speed curve (s) = ( ,  ,  ):
2
1
3
 9 1 sin 36s
1
   208 sin16s  117

 9 1
    cos16s  cos36s
2
 208 117
 6
   sin10s
3
 65
It is rendered in Figure 21.2. And, this curve’s curvature functions are expressed as in [12]:
 K(s)   24sin10s

 T(s)  24cos10s
It is an easy problem to calculate Frenet-Serret apparatus of the unit speed curve  = (s). We also
need
s 24

(s) = 24cos(10s)ds  sin(10s).
0 10
The transformation matrix for the curve  = (s) has the form

 
 1 0 0 
 T    24 24    T 
  cos( sin10s) sin( sin10s)  
N 
   0  10 10    M 1 
  24 24  M 
B
    sin( sin10s) cos( sin10s)   2 
0  10 10 
 
 
Figure 21.2: Tangent, M and M Bishop Spherical Images of  = (s) for a = 12; b = 5 and c = 13.
1
2

254 LOVELY PROFESSIONAL UNIVERSITY