Page 74 - DCOM303_DMGT504_OPERATION_RESEARCH

Unit 3: Linear Programming Problem – Simplex Method

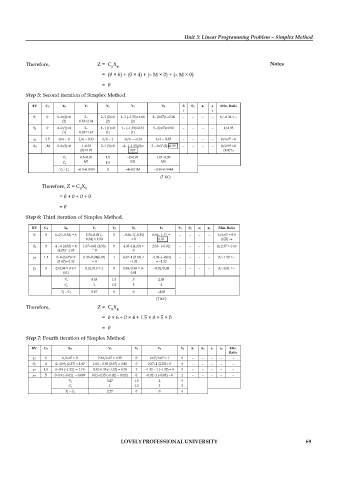
Therefore, Z = C X Notes
B B
= (0 × 6) + (0 × 4) + (– M × 0) + (– M × 0)
= 0
Step 5: Second iteration of Simplex Method.

BV CB XB Y1 Y2 Y3 Y4 S S2 a1 a Min. Ratio
1 2
S1 0 6–0 (2)=6 3– 2–1 (2)=0 4–1 (–1.33)=6.66 1– (0.67)=–0.34 – – – – 6/–0.34 = –
(2) 0.33=2.34 (2) (2)
S2 0 4–0 (1)=4 2– 1–1 (1)=0 1– (–1.33)=2.33 5– (0.67)=0.92 – – – – 4/4.33
(1) 0.33=1.67 (1) (1)
y2 1.5 0/6 = 0 2/6 = 0.33 6/6 = 1 –8/6 = –1.33 4/6 = 0.67 – – – – 0/0.67 = 0
A2 –M 0–0 (3)=0 1–0.33 3–1 (3)=0 –4– (–1.33)(3)= 3 – 0.67 (3)=0.99 – – – – 0/0.99 = 0
(3)=0.01 0.01 (KR)?
Zj 0.5–0.01 1.5 –2+0.01 1.01–0.99
Cj M1 1.5 M2 M5
Zj – Cj –0.5–0.01M 0 –4+0.01M –3.99–0.99M
( KC)
Therefore, Z = C X
B B
= 0 + 0 + 0 + 0
= 0
Step 6: Third iteration of Simplex Method.

BV CB XB Y1 Y2 Y3 Y4 S1 S2 a1 a2 Min. Ratio
S1 0 6–0 (–0.34) = 6 2.34–0.01 (– 0 –0.34–1(–0.34) 6.66– (–1) = – – – – 6/6.67 = 0.9
0.34) = 2.34 = 0 6.67 (KR) 
S2 0 4 – 0 (4.33) = 4 1.67–0.01 (4.33) 0 4.33–1(4.33) = 2.33– (–0.01) – – – – 4/2.37 = 1.69
(4.33)= 1.63 = 0 0
y2 1.5 0–0 (0.67)= 0 0.33–0.01(0.67) 1 0.67–1 (0.67) = –1.33–(–0.01) – – – – 0/–1.32 = –
(0.67)= 0.32 = 0 –1.32 = –1.32
y4 5 0/0.99 = 0 9 = 0.01/0.9 = 1 0 0.99/0.99 = 0– –0.01/0.09 – – – – 0/–0.01 = –
0.01 0.01
Zj 0.53 1.5 5 2.03
Cj 1 1.5 5 2
Zj – Cj 0.47 0 0 –4.03
( KC)
Therefore, Z = C X
B B
= 0 × 6 + 0 × 4 + 1.5 × 0 + 5 × 0
= 0

Step 7: Fourth iteration of Simplex Method
BV CB XB Y1 Y2 Y3 Y4 S1 S2 a1 a2 Min.
Ratio
y3 2 6/6.67 = 0 2.34/6.67 = 0.35 0 6.67/6.67 = 1 0 – – – – –
S2 0 4– (0.9) (2.37) = 1.87 1.63 – 0.35 (2.37) = 0.80 0 2.37–1 (2.37)= 0 0 – – – – –
y2 1.5 0–0.9 (–1.32) = 1.19 0.32–0.35 (–1.32) = 0.78 1 –1.32 – 1 (–1.32) = 0 0 – – – – –
y4 5 0–0.9 (–0.01) = 0.009 0.01–0.35 (–0.01) = 0.014 0 –0.01–1 (–0.01) = 0 1 – – – – –
Zj 3.27 1.5 2 5
Cj 1 1.5 2 5
Zj – Cj 2.27 0 0 0

LOVELY PROFESSIONAL UNIVERSITY 69