Page 180 - DCAP108_DIGITAL_CIRCUITS_AND_LOGIC_DESIGNS

Unit 10: Clocked Sequential Circuits

Notes
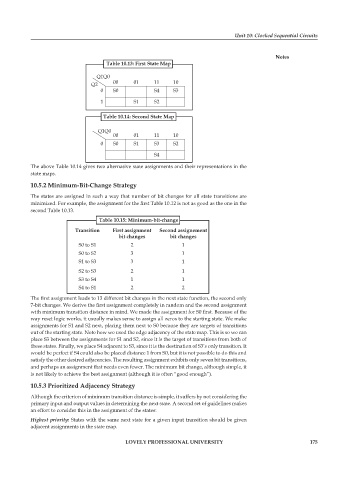
Table 10.13: First State Map

Q1Q0
Q2 00 01 11 10
0 S0 S4 S3

1 S1 S2

Table 10.14: Second State Map

Q1Q0
00 01 11 10
0 S0 S1 S3 S2
S4

The above Table 10.14 gives two alternative state assignments and their representations in the
state maps.

10.5.2 Minimum-Bit-Change Strategy
The states are assigned in such a way that number of bit changes for all state transitions are
minimized. For example, the assignment for the first Table 10.12 is not as good as the one in the
second Table 10.13.

Table 10.15: Minimum-bit-change
Transition First assignment Second assignement
bit changes bit changes
S0 to S1 2 1
S0 to S2 3 1
S1 to S3 3 1

S2 to S3 2 1
S3 to S4 1 1
S4 to S1 2 2

The first assignment leads to 13 different bit changes in the next state function, the second only
7-bit changes. We derive the first assignment completely in random and the second assignment
with minimum transition distance in mind. We made the assignment for S0 first. Because of the
way reset logic works, it usually makes sense to assign all zeros to the starting state. We make
assignments for S1 and S2 next, placing them next to S0 because they are targets of transitions
out of the starting state. Note how we used the edge adjacency of the state map. This is so we can
place S3 between the assignments for S1 and S2, since it is the target of transitions from both of
these states. Finally, we place S4 adjacent to S3, since it is the destination of S3’s only transition. It
would be perfect if S4 could also be placed distance 1 from S0, but it is not possible to do this and
satisfy the other desired adjacencies. The resulting assignment exhibits only seven bit transitions,
and perhaps an assignment that needs even fewer. The minimum bit change, although simple, it
is not likely to achieve the best assignment (although it is often “good enough”).

10.5.3 Prioritized Adjacency Strategy
Although the criterion of minimum transition distance is simple, it suffers by not considering the
primary input and output values in determining the next state. A second set of guidelines makes
an effort to consider this in the assignment of the states:
Highest priority: States with the same next state for a given input transition should be given
adjacent assignments in the state map.

LOVELY PROFESSIONAL UNIVERSITY 175