Page 17 - DCAP210_INTRODUCTION__TO_MICROPROCESSORS

Unit 1: Microprocessors and Microcomputers

The computing performance of a computer system cannot be easily measured, nor can it be related Notes
in a simple manner to the number of transistors in the processor itself. Indeed, the only widely
used measures of performance are various benchmark programs, which serve to provide
essentially ordinal comparisons of relative performance for complete systems running a specific
benchmark. This is for good reasons, since the speed with which any machine can solve a given
problem depends upon the internal architecture of the system, the internal micro architecture of
the processor chip itself, the internal bandwidth of the buses, the speed and size of the main

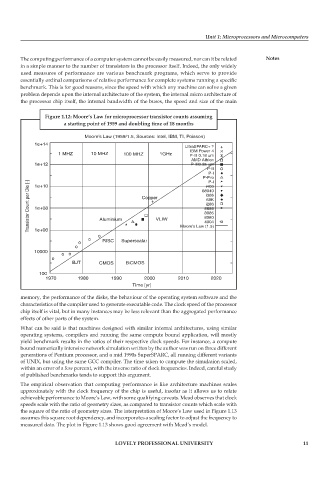
Figure 1.12: Moore’s Law for microprocessor transistor counts assuming
a starting point of 1959 and doubling time of 18 months

memory, the performance of the disks, the behaviour of the operating system software and the
characteristics of the compiler used to generate executable code. The clock speed of the processor
chip itself is vital, but in many instances may be less relevant than the aggregated performance
effects of other parts of the system.

What can be said is that machines designed with similar internal architectures, using similar
operating systems, compilers and running the same compute bound application, will mostly
yield benchmark results in the ratios of their respective clock speeds. For instance, a compute
bound numerically intensive network simulation written by the author was run on three different
generations of Pentium processor, and a mid 1990s SuperSPARC, all running different variants
of UNIX, but using the same GCC compiler. The time taken to compute the simulation scaled,
within an error of a few percent, with the inverse ratio of clock frequencies. Indeed, careful study
of published benchmarks tends to support this argument.
The empirical observation that computing performance is like architecture machines scales
approximately with the clock frequency of the chip is useful, insofar as it allows us to relate
achievable performance to Moore’s Law, with some qualifying caveats. Mead observes that clock
speeds scale with the ratio of geometry sizes, as compared to transistor counts which scale with
the square of the ratio of geometry sizes. The interpretation of Moore’s Law used in Figure 1.13
assumes this square root dependency, and incorporates a scaling factor to adjust the frequency to
measured data. The plot in Figure 1.13 shows good agreement with Mead’s model.

LOVELY PROFESSIONAL UNIVERSITY 11