Page 247 - DMGT501_OPERATIONS_MANAGEMENT

Unit 10: Economic Order Quantity

Notes
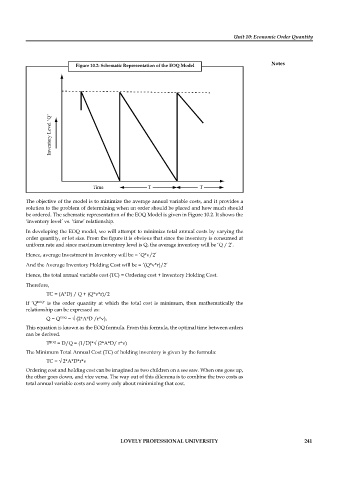
Figure 10.2: Schematic Representation of the EOQ Model

The objective of the model is to minimize the average annual variable costs, and it provides a
solution to the problem of determining when an order should be placed and how much should
be ordered. The schematic representation of the EOQ Model is given in Figure 10.2. It shows the
‘inventory level’ vs. ‘time’ relationship.
In developing the EOQ model, we will attempt to minimize total annual costs by varying the

order quantity, or lot size. From the figure it is obvious that since the inventory is consumed at
uniform rate and since maximum inventory level is Q, the average inventory will be ‘Q / 2’.
Hence, average Investment in Inventory will be = ‘Q*v/2’

And the Average Inventory Holding Cost will be = ‘(Q*v*r)/2’
Hence, the total annual variable cost (TC) = Ordering cost + Inventory Holding Cost.
Therefore,
TC = (A*D) / Q + (Q*v*r)/2
If ‘Q EOQ ’ is the order quantity at which the total cost is minimum, then mathematically the
relationship can be expressed as:
Q = Q EOQ = √ (2*A*D /r*v),
This equation is known as the EOQ formula. From this formula, the optimal time between orders
can be derived.
T EOQ = D/Q = (1/D)*√ (2*A*D/ r*v)
The Minimum Total Annual Cost (TC) of holding inventory is given by the formula:
TC = √ 2*A*D*r*v
Ordering cost and holding cost can be imagined as two children on a see saw. When one goes up,
the other goes down, and vice versa. The way out of this dilemma is to combine the two costs as
total annual variable costs and worry only about minimizing that cost.

LOVELY PROFESSIONAL UNIVERSITY 241