Page 251 - DMGT501_OPERATIONS_MANAGEMENT

Unit 10: Economic Order Quantity

Notes
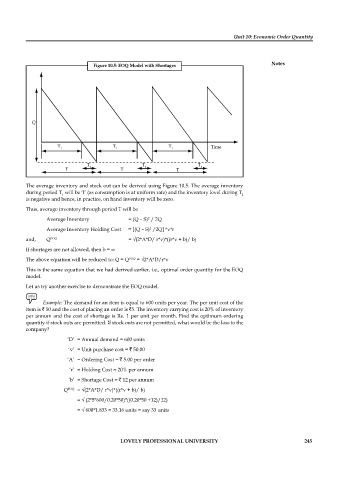
Figure 10.5: EOQ Model with Shortages

The average inventory and stock out can be derived using Figure 10.5. The average inventory
during period T will be ‘I’ (as consumption is at uniform rate) and the inventory level during T
1 2
is negative and hence, in practice, on hand inventory will be zero.
Thus, average inventory through period T will be

Average Inventory = (Q – S) / 2Q
2
2
Average Inventory Holding Cost = [(Q – S) /2Q] *v*r
and, Q EOQ = √(2*A*D/ r*v)*((r*v + b)/ b)
If shortages are not allowed, then b = ∞
The above equation will be reduced to: Q = Q EOQ = √2*A*D/r*v

This is the same equation that we had derived earlier, i.e., optimal order quantity for the EOQ
model.
Let us try another exercise to demonstrate the EOQ model.

Example: The demand for an item is equal to 600 units per year. The per unit cost of the
item is 50 and the cost of placing an order is 5. The inventory carrying cost is 20% of inventory
per annum and the cost of shortage is Re. 1 per unit per month. Find the optimum ordering
quantity if stock outs are permitted. If stock outs are not permitted, what would be the loss to the
company?
‘D’ = Annual demand = 600 units
‘v’ = Unit purchase cost = 50.00
‘A’ = Ordering Cost = 5.00 per order

‘r’ = Holding Cost = 20% per annum
‘b’ = Shortage Cost = 12 per annum
Q EOQ = √(2*A*D/ r*v)*((r*v + b)/ b)
= √ (2*5*600/0.20*50)*((0.20*50 +12)/12)
= √ 600*1.833 = 33.16 units = say 33 units

LOVELY PROFESSIONAL UNIVERSITY 245