Page 235 - DMGT524_TOTAL_QUALITY_MANAGEMENT

Total Quality Management

Notes
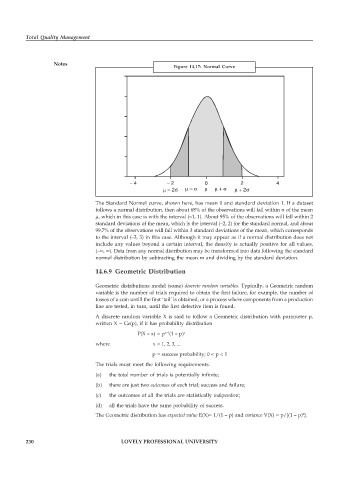
Figure 14.17: Normal Curve

– 4 – 2 0 2 4
m – 2s m – s m m + s m + 2s

The Standard Normal curve, shown here, has mean 0 and standard deviation 1. If a dataset
follows a normal distribution, then about 68% of the observations will fall within σ of the mean
μ, which in this case is with the interval (–1, 1). About 95% of the observations will fall within 2
standard deviations of the mean, which is the interval (–2, 2) for the standard normal, and about
99.7% of the observations will fall within 3 standard deviations of the mean, which corresponds
to the interval (–3, 3) in this case. Although it may appear as if a normal distribution does not
include any values beyond a certain interval, the density is actually positive for all values,
(–∞, ∞). Data from any normal distribution may be transformed into data following the standard
normal distribution by subtracting the mean m and dividing by the standard deviation.

14.6.9 Geometric Distribution

Geometric distributions model (some) discrete random variables. Typically, a Geometric random
variable is the number of trials required to obtain the first failure, for example, the number of
tosses of a coin untill the first ‘tail’ is obtained, or a process where components from a production
line are tested, in turn, until the first defective item is found.
A discrete random variable X is said to follow a Geometric distribution with parameter p,
written X ~ Ge(p), if it has probability distribution

x–1
P(X = x) = p (1 – p) x
where x = 1, 2, 3, ...
p = success probability; 0 < p < 1
The trials must meet the following requirements:

(a) the total number of trials is potentially infinite;
(b) there are just two outcomes of each trial; success and failure;
(c) the outcomes of all the trials are statistically independent;
(d) all the trials have the same probability of success.
2
The Geometric distribution has expected value E(X)= 1/(1 – p) and variance V(X) = p/{(1 – p) }.

230 LOVELY PROFESSIONAL UNIVERSITY