Page 37 - DECO401_MICROECONOMIC_THEORY_HINDI

bdkbZ 3 % miHkksDrk fl¼karμx.kukokpd mi;ksfxrk fo'ys"k.k

uksV
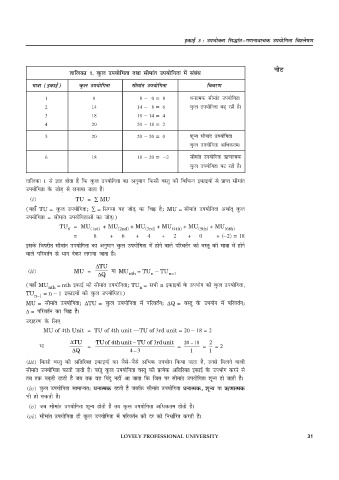
rkfydk 1- oqQy mi;ksfxrk rFkk lhekar mi;ksfxrk esa lacaèk
ek=kk (bdkbZ) oqQy mi;ksfxrk lhekar mi;ksfxrk fooj.k

1 8 8 μ 0 = 8 èkukRed lhekar mi;ksfxrk
2 14 14 μ 8 = 6 oqQy mi;ksfxrk c<+ jgh gSA
3 18 18 μ 14 = 4
4 20 20 μ 18 = 2

5 20 20 μ 20 = 0 'kwU; lhekar mi;ksfxrk
oqQy mi;ksfxrk vfèkdreA
6 18 18 μ 20 = μ2 lhekar mi;ksfxrk ½.kkRed
oqQy mi;ksfxrk ?kV jgh gSA

rkfydk 1 ls Kkr gksrk gS fd oqQy mi;ksfxrk dk vuqeku fdlh oLrq dh fofHkUu bdkb;ksa ls izkIr lhekar
mi;ksfxrk osQ tksM+ ls yxk;k tkrk gSA
(i) TU = ∑ MU

(;gk¡ TU = oqQy mi;ksfxrk_ ∑ = flxek ;g tksM+ dk fpÉ gS_ MU = lhekar mi;ksfxrk vFkkZr~ oqQy
mi;ksfxrk = lhekar mi;ksfxrkvksa dk tksM+A)
TU =MU + MU + MU + MU + MU + MU
6 (1st) (2nd) (3rd) (4th) (5th) (6th)
= 8 + 6 + 4 + 2 + 0 + (–2) = 18

blosQ foijhr lhekar mi;ksfxrk dk vuqeku oqQy mi;ksfxrk esa gksus okys ifjorZu dks oLrq dh ek=kk esa gksus
okys ifjorZu ls Hkkx nsdj yxk;k tkrk gSA

ΔTU
(ii) MU = ;k MU = TU – TU
ΔQ nth n n–1
(;gk¡ MU = nth bdkbZ dh lhekar mi;ksfxrk_ TU = lHkh n bdkb;ksa osQ miHkksx dh oqQy mi;ksfxrk]
nth n
TU = n – 1 bdkb;ksa dh oqQy mi;ksfxrkA)
n–1
MU = lhekar mi;ksfxrk_ ΔTU = oqQy mi;ksfxrk esa ifjorZu_ ΔQ = oLrq osQ mi;ksx esa ifjorZu_
Δ = ifjorZu dk fpÉ gSA
mnkgj.k osQ fy,
MU of 4th Unit = TU of 4th unit —TU of 3rd unit = 20 – 18 = 2
ΔTU TUof 4thunit – TU of 3rdunit 20 – 18 2
;k = = = = 2
ΔQ 4–3 1 1
(iii) fdlh oLrq dh vfrfjDr bdkb;ksa dk tSls&tSls vfèkd miHkksx fd;k tkrk gS] muls feyus okyh
lhekar mi;ksfxrk ?kVrh tkrh gSA ijarq oqQy mi;ksfxrk oLrq dh izR;sd vfrfjDr bdkbZ osQ miHkksx djus ls
rc rd c<+rh jgrh gS tc rd og fcanq ugha vk tkrk fd ftl ij lhekar mi;ksfxrk 'kwU; gks tkrh gSA
(iv) oqQy mi;ksfxrk lkekU;r% èkukRed jgrh gS tcfd lhekar mi;ksfxrk èkukRed] 'kwU; ;k ½.kkRed
Hkh gks ldrh gSA
(v) tc lhekar mi;ksfxrk 'kwU; gksrh gS rc oqQy mi;ksfxrk vfèkdre gksrh gSA
(vi) lhekar mi;ksfxrk gh oqQy mi;ksfxrk esa ifjorZu dh nj dks fuèkkZfjr djrh gSA

LOVELY PROFESSIONAL UNIVERSITY 31