Page 35 - DECO504_STATISTICAL_METHODS_IN_ECONOMICS_ENGLISH

Unit 3: Classification and Tabulation of Data: Frequency and Cumulative Frequency Distribution

We have given heights in cms in whole numbers or heights have been recorded to the nearest Notes
centimetre. Thus a height of 144.50 or more but less than 145.5 is recorded as 145; a height of 145.5 or
more but less than 146.5 is recorded as 146 and so on. So the class 145-146 could also be indicated by
144.5-146.5 implying the class which includes any height greater than or equal to 144.5 but less than
146.5; the class 147-148 could be indicated by 146.5-148.5, meaning the class which includes any
height greater than or equal to 146.5 but less than 148.5. Following this convention, the classes could
be represented as: 144.5-146,5, 146.5-148.5, and so on. The above frequency distribution should finally
be represented as follows.
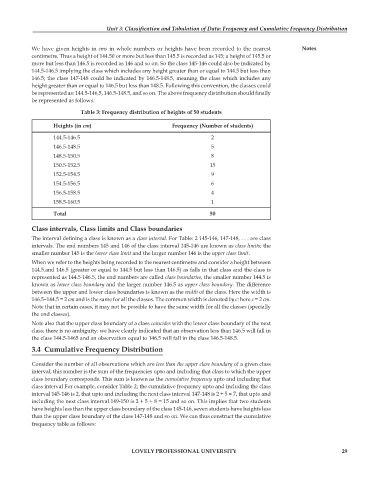
Table 3: Frequency distribution of heights of 50 students

Heights (in cm) Frequency (Number of students)

144.5-146.5 2
146.5-148.5 5
148.5-150.5 8
150.5-152.5 15
152.5-154.5 9
154.5-156.5 6
156.5-158.5 4
158.5-160.5 1
Total 50

Class intervals, Class limits and Class boundaries
The interval defining a class is known as a class interval. For Table: 2 145-146, 147-148, . . . are class
intervals. The end numbers 145 and 146 of the class interval 145-146 are known as class limits; the
smaller number 145 is the lower class limit and the larger number 146 is the upper class limit.
When we refer to the heights being recorded to the nearest centimetre and consider a height between
144.5.and 146.5 (greater or equal to 144.5 but less than 146.5) as falls in that class and the class is
represented as 144.5-146.5, the end numbers are called class boundaries, the smaller number 144.5 is
known as lower class boundary and the larger number 146.5 as upper class boundary. The difference
between the upper and lower class boundaries is known as the width of the class. Here the width is
146.5–144.5 = 2 cm and is the same for all the classes. The common width is denoted by c: here c = 2 cm.
Note that in certain cases, it may not be possible to have the same width for all the classes (specially
the end classes).
Note also that the upper class boundary of a class coincides with the lower class boundary of the next
class; there is no ambiguity: we have clearly indicated that an observation less than 146.5 will fall in
the class 144.5-1465 and an observation equal to 146.5 will fall in the class 146.5-148.5.
3.4 Cumulative Frequency Distribution

Consider the number of all observations which are less than the upper class boundary of a given class
interval; this number is the sum of the frequencies upto and including that class to which the upper
class boundary corresponds. This sum is known as the cumulative frequency upto and including that
class interval For example, consider Table 2; the cumulative frequency upto and including the class
interval 145-146 is 2, that upto and including the next class interval 147-148 is 2 + 5 = 7, that upto and
including the next class interval 149-150 is 2 + 5 + 8 = 15 and so on. This implies that two students
have heights less than the upper class boundary of the class 145-146, seven students have heights less
than the upper class boundary of the class 147-148 and so on. We can thus construct the cumulative
frequency table as follows:

LOVELY PROFESSIONAL UNIVERSITY 29