Page 34 - DECO504_STATISTICAL_METHODS_IN_ECONOMICS_ENGLISH

Statistical Methods in Economics

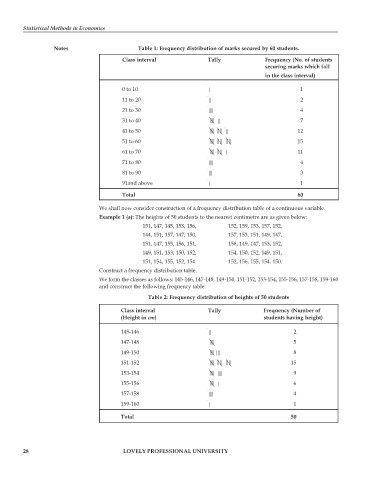
Notes Table 1: Frequency distribution of marks secured by 60 students.

Class interval Tally Frequency (No. of students
securing marks which fall
in the class interval)

0 to 10 | 1
11 to 20 || 2
21 to 30 |||| 4
31 to 40 |||| || 7
41 to 50 |||| |||| || 12
51 to 60 |||| |||| |||| 15

61 to 70 |||| |||| | 11
71 to 80 |||| 4
81 to 90 ||| 3
91and above | 1

Total 60
We shall now consider construction of a frequency distribution table of a continuous variable.
Example 1 (a): The heights of 50 students to the nearest centimetre are as given below:
151, 147, 145, 153, 156, 152, 159, 153, 157, 152,
144, 151, 157, 147, 150, 157, 153, 151, 149, 147,
151, 147, 155, 156, 151, 158, 149, 147, 153, 152,
149, 151, 153, 150, 152, 154, 150, 152, 149, 151,
151, 154, 155, 152, 154 152, 156, 155, 154, 150.
Construct a frequency distribution table.
We form the classes as follows: 145-146, 147-148, 149-150, 151-152, 153-154, 155-156, 157-158, 159-160
and construct the following frequency table:

Table 2: Frequency distribution of heights of 50 students
Class interval Tally Frequency (Number of
(Height in cm) students having height)

145-146 || 2
147-148 |||| 5
149-150 |||| ||| 8
151-152 |||| |||| |||| 15
153-154 |||| |||| 9
155-156 |||| | 6
157-158 |||| 4

159-160 | 1
Total 50

28 LOVELY PROFESSIONAL UNIVERSITY