Page 36 - DECO504_STATISTICAL_METHODS_IN_ECONOMICS_ENGLISH

Statistical Methods in Economics

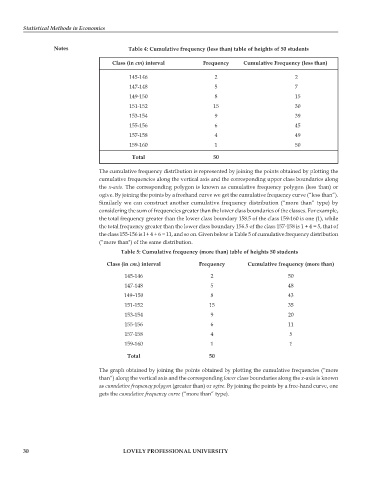
Notes Table 4: Cumulative frequency (less than) table of heights of 50 students

Class (in cm) interval Frequency Cumulative Frequency (less than)

145-146 2 2
147-148 5 7
149-150 8 15
151-152 15 30
153-154 9 39
155-156 6 45
157-158 4 49
159-160 1 50

Total 50

The cumulative frequency distribution is represented by joining the points obtained by plotting the
cumulative frequencies along the vertical axis and the corresponding upper class boundaries along
the x-axis. The corresponding polygon is known as cumulative frequency polygon (less than) or
ogive. By joining the points by a freehand curve we get the cumulative frequency curve (“less than”).
Similarly we can construct another cumulative frequency distribution (“more than” type) by
considering the sum of frequencies greater than the lower class boundaries of the classes. For example,
the total frequency greater than the lower class boundary 158.5 of the class 159-160 is one (1), while
the total frequency greater than the lower class boundary 156.5 of the class 157-158 is 1 + 4 = 5, that of
the class 155-156 is I + 4 + 6 = 11, and so on. Given below is Table 5 of cumulative frequency distribution
(“more than") of the same distribution.
Table 5: Cumulative frequency (more than) table of heights 50 students

Class (in cm.) interval Frequency Cumulative frequency (more than)
145-146 2 50
147-148 5 48
149–150 8 43
151-152 15 35
153-154 9 20
155-156 6 11
157-158 4 5
159-160 1 1

Total 50

The graph obtained by joining the points obtained by plotting the cumulative frequencies (“more
than”) along the vertical axis and the corresponding lower class boundaries along the x-axis is known
as cumulative frequency polygon (greater than) or ogive. By joining the points by a free-hand curve, one
gets the cumulative frequency curve (“more than” type).

30 LOVELY PROFESSIONAL UNIVERSITY