Page 218 - DMTH404_STATISTICS

Statistics

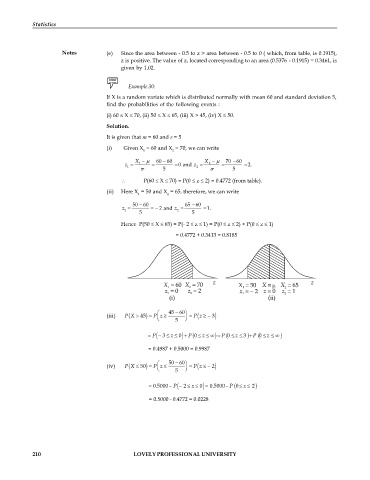
Notes (e) Since the area between - 0.5 to z > area between - 0.5 to 0 ( which, from table, is 0.1915),
z is positive. The value of z, located corresponding to an area (0.5376 - 0.1915) = 0.3461, is
given by 1.02.

Example 30:

If X is a random variate which is distributed normally with mean 60 and standard deviation 5,
find the probabilities of the following events :
(i) 60 £ X £ 70, (ii) 50 £ X £ 65, (iii) X > 45, (iv) X £ 50.

Solution.
It is given that m = 60 and s = 5
(i) Given X = 60 and X = 70, we can write
1 2
X - m 60 60 X - m 70 60
-
-
z = 1 = = 0 and z = 2 = = 2.
1 2
 5  5
 P(60 £ X £ 70) = P(0 £ z £ 2) = 0.4772 (from table).
(ii) Here X = 50 and X = 65, therefore, we can write
1 2
50 60 65 60
-
-
z = = - 2 and z = = 1.
1 2
5 5
Hence P(50 £ X £ 65) = P(- 2 £ z £ 1) = P(0 £ z £ 2) + P(0 £ z £ 1)
= 0.4772 + 0.3413 = 0.8185

-
æ 45 60ö
(iii) P (X > 45 ) = ç ÷ = P (z  - ) 3
P z 
è 5 ø
)
z
P= ( 3- £ £ ) 0 + P (0 £ £ ¥ = P ( 0 £ £ ) 3 + P ( 0 £ £ ¥ )
z
z
z
= 0.4987 + 0.5000 = 0.9987
-
æ 50 60ö
(iv) P (X £ 50 ) = ç ÷ = P (z £ - ) 2
P z £
è 5 ø
z
0.5000 P= - ( 2 z- £ £ ) 0 = 0.5000 P ( 0 £ £ ) 2
-
= 0.5000 - 0.4772 = 0.0228

210 LOVELY PROFESSIONAL UNIVERSITY