Page 269 - DECO401_MICROECONOMIC_THEORY_HINDI

bdkbZ 11 % vk; ;k vkxe dh /kj.kk,¡

8 #i, izkIr gksxhA blls izdV gksrk gS fd nwljh bdkbZ dh lhekar vk; 'kwU; (Zero) gksxhA fp=k esa OX- uksV
v{k dks gh MR oØ ekuk x;k gSA

fp=k 11-3

Y

6
Revenue 4 P

N
2
AR
0 MR X
2 4 6
Output

11-6 oqQy vkSlr rFkk lhekar vkxe esa T;kferh; ;k xzkfiQd laca/
(Graphical or Geometrical Relation between Total, Average
and Marginal Revenues)

,d iQeZ osQ oqQy] vkSlr rFkk lhekar vkxeksa esa fuEufyf[kr eq[; lacaèk gSaμ

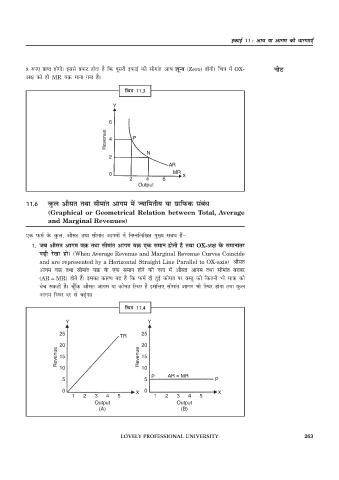
1- tc vkSlr vkxe oØ rFkk lhekar vkxe oØ ,d leku gksrh gS rFkk OX-v{k osQ lekukarj
iM+h js[kk gksA (When Average Revenue and Marginal Revenue Curves Coincide
and are represented by a Horizontal Straight Line Parallel to OX-axis) vkSlr
vkxe oØ rFkk lhekar oØ osQ ,d leku gksus dh n'kk esa vkSlr vkxe rFkk lhekar cjkcj
(AR = MR) gksrs gSaA bldk dkj.k ;g gS fd iQeZ nh gqbZ dher ij oLrq dh fdruh Hkh ek=kk dks
csp ldrh gSA pw¡fd vkSlr vkxe ;k dher fLFkj gS blfy, lhekar vkxe Hkh fLFkj gksxk rFkk oqQy
vkxe fLFkj nj ls c<+sxkA

fp=k 11-4

Y Y

25 25
TR
20 20
Revenue 15 Revenue 15

10 10
P AR = MR
5 5 P
0 X 0 X
1 2 3 4 5 1 2 3 4 5
Output Output
(A) (B)

LOVELY PROFESSIONAL UNIVERSITY 263